P6493 [COCI 2010/2011 #6] VODA
题目描述
在一个 $r\times s$ 的网格城市里,你承担着水资源运输的设计工作。
具体来说,你需要把水资源从左上角 $(1,1)$ 的上方运输到右下角 $(r,s)$ 的下方,通过铺设水管来实现。
有些格子为 `#`,表示有障碍物,无法铺设水管;其他的格子为 `.`,表示可以铺设水管。每一个为 `.` 的格子都可以铺设如下六种水管之一(也可以不铺设水管):
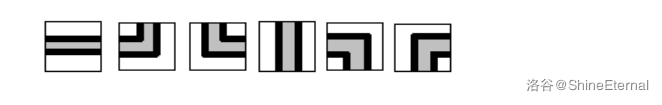
你需要求出共有多少种可能的设计方案($\bmod\ 10007$)。使得水资源在运输的过程中不漏出水管且所有铺设在城市中的水管都被使用。
输入格式
输入第一行两个整数 $r,s$,表示城市的行数和列数。
接下来的 $r$ 行,每行 $s$ 个字符,其中 `#` 表示无法铺设水管,`.` 表示可以铺设水管。
输出格式
输出一行一个整数,表示总方案数($\bmod\ 10007$)。
说明/提示
#### 样例 1 解释
对于第一个样例,只有如下图这一种铺设方案:

#### 数据规模与约定
对于 $100\%$ 的数据,保证 $2\le r,s\le 10$。
#### 说明
**题目译自 [COCI2010-2011](https://hsin.hr/coci/archive/2010_2011/) [CONTEST #6](https://hsin.hr/coci/archive/2010_2011/contest6_tasks.pdf) *T6 VODA***。