P6493 [COCI 2010/2011 #6] VODA

In an $r \times s$ grid city, you are responsible for designing the water transportation system. More specifically, you need to transport water from above the top-left corner $(1,1)$ to below the bottom-right corner $(r,s)$ by laying pipes. Some cells are `#`, meaning there are obstacles and pipes cannot be placed there. The other cells are `.`, meaning pipes can be placed. 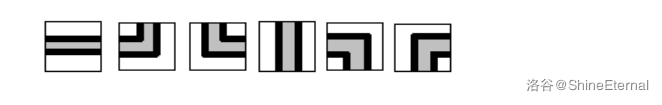Each `.` cell can contain one of the following six types of pipes (or you may place no pipe at all):  You need to find the total number of possible designs ($\bmod\ 10007$), such that during transportation the water does not leak out of the pipes, and every pipe placed in the city is used.

The first line contains two integers $r, s$, representing the number of rows and columns of the city. The next $r$ lines each contain $s$ characters: `#` means a pipe cannot be placed, and `.` means a pipe can be placed.

Output one integer, the total number of designs ($\bmod\ 10007$).

#### Sample 1 Explanation For the first sample, there is only one valid layout as shown below:  #### Constraints For $100\%$ of the testdata, it is guaranteed that $2 \le r, s \le 10$. #### Notes **Translated from [COCI2010-2011](https://hsin.hr/coci/archive/2010_2011/) [CONTEST #6](https://hsin.hr/coci/archive/2010_2011/contest6_tasks.pdf) *T6 VODA***。 Translated by ChatGPT 5