P6513 [QkOI#R1] Quark and Tree
题目描述
给定一棵包含 $n$ 个节点的树,每个节点上有一个点权,点的编号为 $1\sim n$,请加一条不存在于给定的树中的边(且不能为自环),使加边后得到的基环树上所有点的深度与该点点权乘积之和最大。
我们认为基环树上的点的深度指该节点到环上的最短距离,特别地,环上的节点深度为 $0$。
形式化地,你需要添加一条不存在于给定的树中的边(且不能为自环),并最大化:
$$\sum_{i=1}^nw_i\times dep_i$$
其中 $w_i$ 为节点 $i$ 的权值,$dep_i$ 为节点 $i$ 在基环树中的深度。
输入格式
第一行包含一个整数 $n$,表示树中点的个数。
第二行包含 $n$ 个整数,第 $i$ 个整数表示节点 $i$ 的点权 $w_i$。
接下来 $n-1$ 行,一行两个整数 $a_i,b_i$,表示 $a_i$ 和 $b_i$ 在树中有一条边连接。
输出格式
输出包含一行一个整数,表示加边后生成的基环树中,各个节点的深度与其点权乘积之和的最大值。
说明/提示
### 样例解释
样例 1 给出的树如下图所示:
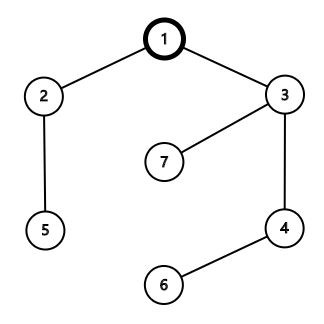
可以添加边 $(1,5)$,则新生成的基环树如下图所示:
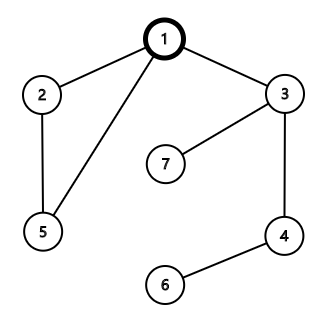
各节点深度见下表:

### 数据范围
**本题采用捆绑测试。**
对于所有数据,$3 \le n \le 10^6$,$-10^3 \le w_i \le 10^3$,$1 \le a_i,b_i \le n$。
+ 子任务 $1$($10$ 分):$n \le 200$。
+ 子任务 $2$($20$ 分):$n \le 10^3$。
+ 子任务 $3$($40$ 分):$w_i \ge 0$。
+ 子任务 $4$($30$ 分):无特殊限制。