P6513 [QkOI#R1] Quark and Tree

Given a tree with $n$ nodes, each node has a weight. The nodes are numbered from $1$ to $n$. Please add one edge that does not exist in the given tree (and it must not be a self-loop), so that in the unicyclic graph formed after adding the edge, the sum of (depth of each node) times (its weight) is maximized. We define the depth of a node in the unicyclic graph as the shortest distance from that node to the cycle. In particular, nodes on the cycle have depth $0$. Formally, you need to add an edge that does not exist in the given tree (and it must not be a self-loop), and maximize: $$\sum_{i=1}^nw_i\times dep_i$$ where $w_i$ is the weight of node $i$, and $dep_i$ is the depth of node $i$ in the unicyclic graph.

The first line contains an integer $n$, indicating the number of nodes in the tree. The second line contains $n$ integers. The $i$-th integer denotes the node weight $w_i$ of node $i$. The next $n-1$ lines each contain two integers $a_i, b_i$, indicating that there is an edge between $a_i$ and $b_i$ in the tree.

Output one integer in a single line, representing the maximum value of the sum of (each node’s depth) times (its weight) in the unicyclic graph after adding the edge.

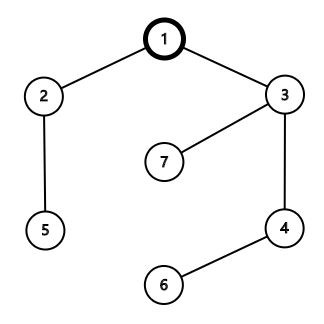
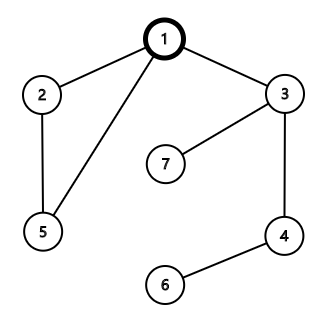
### Sample Explanation The tree given in Sample 1 is shown in the figure below:  You can add the edge $(1,5)$. The resulting unicyclic graph is shown below:  The depths of all nodes are shown in the table below:  ### Constraints **This problem uses bundled testdata.** For all testdata, $3 \le n \le 10^6$, $-10^3 \le w_i \le 10^3$, $1 \le a_i,b_i \le n$. + Subtask $1$ ($10$ points): $n \le 200$. + Subtask $2$ ($20$ points): $n \le 10^3$. + Subtask $3$ ($40$ points): $w_i \ge 0$. + Subtask $4$ ($30$ points): no special constraints. Translated by ChatGPT 5