P6545 [CEOI 2014] The Wall

CEOI 2014 Day 2 T3. Translator: Xiaofentu.

Rectos Island is often hit by floods and attacked by pirates, so the King of Rectos wants to build a wall to protect all villages on the island. Rectos is a rectangular island, so the wall designer views the island as a square grid. Each village is located in one cell of the grid, and the capital village is located at the northwest corner of the whole island, i.e., the top-left cell. It must be guaranteed that from the outside (i.e., outside the entire grid), it is impossible to reach any village without crossing the wall. The designer plans to build the wall only along grid lines. More specifically, he places the first segment of the wall on one of the two grid lines extending from the top-left corner, and each next segment is always connected end-to-end with the previous segment. This process is repeated until it returns to the top-left corner again. This may cause more than one segment of wall to be placed on the same grid edge. In summary, the wall is built as a continuous closed curve along the grid lines. Survey data show that building one segment of wall on each grid edge costs a certain amount. The total cost is the sum of the costs of all wall segments. If $t$ wall segments are built on a certain grid edge, then its cost is counted $t$ times. The King wants to build the wall with as little money as possible. Please help the King: given the positions of the villages and the building cost on each grid edge, compute the minimum total cost needed to build the wall.

The first line contains two positive integers $n, m$, representing the number of rows and columns of the grid. Then follow $n$ lines, each containing $m$ numbers, each being $0$ or $1$. If it is $0$, the cell has no village; if it is $1$, the cell has a village. It is guaranteed that the first number in the first row is $1$. Then follow $n$ lines, each containing $m + 1$ non-negative integers, describing in order the building cost on each vertical grid edge. Then follow $n + 1$ lines, each containing $m$ non-negative integers, describing in order the building cost on each horizontal grid edge.

Output one line with one number, representing the minimum cost to build the wall.

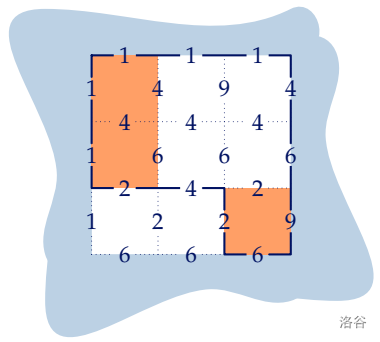
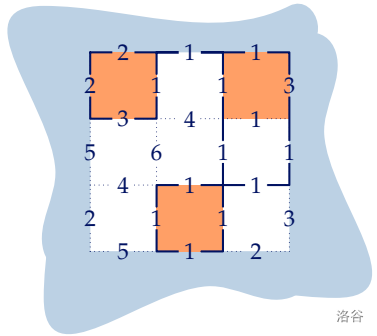
**[Sample #1 Explanation]**  **[Sample #2 Explanation]**  **[Constraints and Notes]** For all testdata, $1 \le n, m \le 400$. For every building cost $v$, $1 \le v \le {10}^9$. | Subtask ID | Score | Special Constraints | | :-: | :-: | :-: | | $1$ | $30$ | $n, m \le 40$ and the number of villages does not exceed $10$ | | $2$ | $30$ | $n, m \le 40$ | | $3$ | $40$ | No special constraints | Translated by ChatGPT 5