P6551 [COCI 2010/2011 #2] CRNI
题目描述
尽管 Mirko 找到了所有最有趣的游乐设施,但他的热情仍然没有消失。 他打开方格纸笔记本,开始给方块上色,一个新的甚至更难的问题浮现在他身上。
您将得到一个 $n \times n$ 的表格。 每个单元格的颜色是黑色或白色。
如果表格内的某一个矩形图形的所有单元格均为黑色并且此矩形由至少两个单元格组成,则此矩形称为黑色矩形。
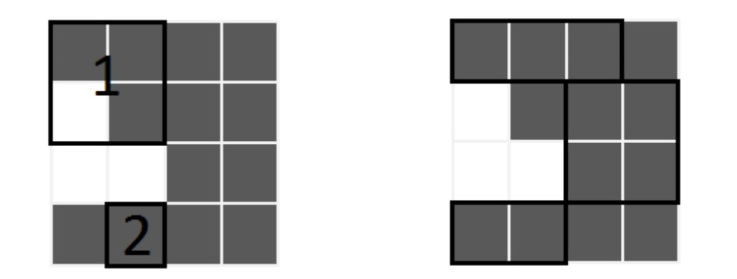
上左图举了两个不是黑色矩形的例子。 标为 $1$ 的矩形不是黑色矩形,因为它包含一个白色单元格;标为 $2$ 的矩形不是黑色矩形,因为它仅包含一个单元格。 上右图则举了三个黑色矩形的例子。
计算选择两个没有公共单元格的黑色矩形的方法数。 由于所求的结果可能非常大,因此您应该输出该数除以 $10^4 + 7$ 后的余数。
输入格式
第一行一个整数 $n$,具体含义请见题目描述。
接下来 $n$ 行,每行一个长度为 $n$ 的大写字符串(由 `C`(表示该单元格颜色为黑)和 `B`(表示该单元格颜色为白)两种字符组成),表示表格。
输出格式
一行一个整数,表示所求方法数除以 $10^4 + 7$ 后的余数。
说明/提示
#### 数据规模与约定
对于 $100\%$ 的数据,保证 $2 \leq n \leq 1 \times 10^3$,输入字符串的每一位只可能是 `C` 或 `B`,令 $|s|$ 为每个字符串长度,则 $|s| = n$。
#### 说明
- 本题满分 $130$ 分。
- 题目译自 [COCI2010-2011](https://hsin.hr/coci/archive/2010_2011/) [CONTEST #2](https://hsin.hr/coci/archive/2010_2011/contest2_tasks.pdf) CRNI,译者 @[mnesia](https://www.luogu.com.cn/user/115711)。