P6556 The Forest

Deep in the forest, swift in the night. They come out, with frightening shouts under the moonlight. You stare at those horrible figures. They are real, alive. I promise you have never had a worse night. They come closer and closer, until only one meter is left. You see their real faces. Scary eyes and messy hair. You think they are coming for you, but you are wrong. They only want your delicious cheese, which is produced on a scary farm. That is what happens in the forest. Enjoy your time!

**Please note that the time limit for this problem is 5s!** Explorer A and Explorer B need to use light bulbs to light up this forest. There are $n$ light bulbs, numbered $1, 2, \cdots, n$. Explorer A uses $n - 1$ red ropes to connect them into a tree, and Explorer B uses $n - 1$ blue ropes to connect them into another tree. At the beginning, all bulbs are off. Now we want to turn on some of the bulbs. Explorer A likes connected components, and Explorer B likes paths. They want to know: how many ways are there to turn on bulbs such that the turned-on bulbs form a connected component in A's tree, and form a path in B's tree?

The first line contains an integer $T$, meaning there are $T$ test cases. For each test case: The first line contains an integer $n$. Lines $2$ to $n$, i.e. line $i + 1$, contain two integers $a_i, b_i$, representing an edge in A's tree. Lines $n + 1$ to $2n - 1$, i.e. line $i + n$, contain two integers $c_i, d_i$, representing an edge in B's tree.

Output $T$ lines. The $i$-th line is the answer for the $i$-th test case.

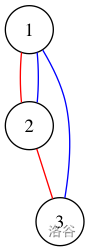
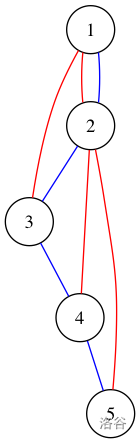
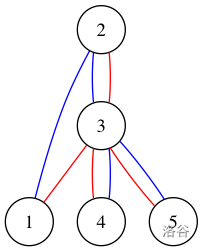
### Sample Explanation: #### Diagrams for the three test cases: **Sample 1:**  **Sample 2:**  **Sample 3:**  ------ For the first test case, the valid sets of bulbs to turn on are: + $\{1\}$; + $\{2\}$; + $\{3\}$; + $\{1, 2\}$; + $\{1, 2, 3\}$. Note that you cannot turn on the set $\{1, 3\}$, because bulbs $1$ and $3$ do not form a connected component in A's tree. You also cannot turn on the set $\{2, 3\}$, because bulbs $2$ and $3$ do not form a path in B's tree. For the second test case, the valid sets of bulbs to turn on that contain **at least two bulbs** are: + $\{1, 2\}$; + $\{1, 2, 3\}$; + $\{1, 2, 3, 4\}$; + $\{1, 2, 3, 4, 5\}$. Clearly, all bulb sets of size $1$ are valid, so the answer is $4 + 5 = 9$. ### Constraints and Notes: For $20\%$ of the testdata, $n \le 50$, and it satisfies the special constraint $X$. For $40\%$ of the testdata, $n \le 3000$, and it satisfies the special constraint $X$. For $70\%$ of the testdata, it satisfies the special constraint $X$. For $100\%$ of the testdata, $T = 3, 1 \le n \le 10^5$. Special constraint $X$: $c_i = i, d_i = i + 1$, that is, **B's tree** is a path, and there is an edge between nodes with adjacent indices. Translated by ChatGPT 5