P6591 [YsOI2020] Tree Planting

In response to the call, Ysuperman decides to plant trees in a kindergarten.

Ysuperman has an unrooted tree $T$ with $n$ nodes. If you do not know what a tree is, they are happy to tell you that a tree is an undirected connected graph without cycles. Since the tree is unrooted, there is no way to “plant” it. After studying gardening for a long time, Ysuperman finds that for a node to be able to serve as the root, it must be very balanced. This means that when it is chosen as the root, among the nodes **directly connected** to it, the sizes of their subtrees are all the same. As the leader of the kindergarten IT group, given a tree by Ysuperman, can you find all nodes that can possibly be the root within $1\text{s}$?

The first line contains a positive integer $n$, the number of nodes in the tree. The next $n-1$ lines each contain two positive integers $u_i, v_i$, indicating that there is an edge directly connecting $u_i$ and $v_i$ in the tree. It is guaranteed that each edge is given exactly once.

Output at most $n$ integers in increasing order, separated by spaces, representing every node that can possibly be the root.

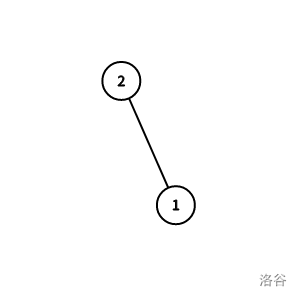
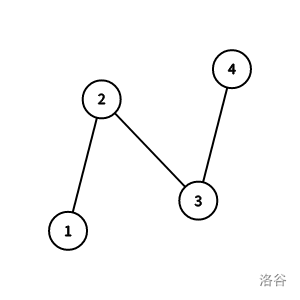
### Sample Explanation #### Sample Explanation $1$.  When rooted at $1$, the nodes directly connected to $1$ are $\{2\}$. Since there is only one, all subtree sizes are the same. When rooted at $2$, the nodes directly connected to $2$ are $\{1\}$. Since there is only one, all subtree sizes are the same. So the answer is $1, 2$. #### Sample Explanation $2$  When rooted at $1$, the nodes directly connected to $1$ are $\{2\}$. Since there is only one, all subtree sizes are the same. When rooted at $2$, the nodes directly connected to $2$ are $\{1, 3\}$. Their subtree sizes are $\{1, 2\}$, which are not the same. When rooted at $3$, the nodes directly connected to $3$ are $\{2, 4\}$. Their subtree sizes are $\{2, 1\}$, which are not the same. When rooted at $4$, the nodes directly connected to $4$ are $\{3\}$. Since there is only one, all subtree sizes are the same. So the answer is $1, 4$. ---- ### Constraints **This problem uses bundled testdata.** | $\rm{subtask}$ | $n$ | Score | | :-----------: | :-----------: | :----: | | $1$ | $\le 5000$ | $40$ | | $2$ | $\le 10^6$ | $60$ | For $100\%$ of the data, $1 \le n \le 10^6$. ------ ### Hint Since the input and output sizes are large, you may need fast I/O. Translated by ChatGPT 5