P6594 [YsOI2020] Changing Dorm Rooms

School is about to start, and Ysuperman is extremely busy assigning dorm rooms to the kids......

There are $n$ rooms in the kindergarten. These rooms are connected by $n-1$ bidirectional roads. The $i$-th road connects rooms $u_i$ and $v_i$. Ysuperman can choose to open or close each road. With all roads open, every room can reach any other room. Each room has a “difference value”. The difference value of room $i$ is $h_i$. After deciding which roads to close, the whole dormitory will be split into several connected components. For a connected component, the kids’ dissatisfaction value is defined as the **maximum difference value minus the minimum difference value** within that component. The kids’ total dissatisfaction value is defined as the **maximum** dissatisfaction value among **all connected components**. There are $m$ dorm teachers. Each teacher checks rooms at night. The $i$-th teacher will walk from room $x_i$ to room $y_i$. If a teacher passes through a closed road during the check, they will be very angry. A teacher’s dissatisfaction value is defined as the **number of closed roads** on the path from $x_i$ to $y_i$. The teachers’ total dissatisfaction value is defined as the **sum** of dissatisfaction values of all teachers. The maximum teachers’ total dissatisfaction value that Ysuperman can tolerate is $k$. Now Ysuperman wants to know the minimum possible value of the kids’ total dissatisfaction value.

The input contains $n+m+1$ lines. The first line contains three integers $n, m, k$, representing the number of rooms, the number of dorm teachers, and the maximum teachers’ total dissatisfaction value that Ysuperman can tolerate. The next line contains $n$ integers. The $i$-th integer is $h_i$, representing the difference value of room $i$. The next $n-1$ lines each contain two integers. Line $i+2$ gives $u_i$ and $v_i$, indicating that there is a direct road between dorms $u_i$ and $v_i$. The next $m$ lines each contain two integers. Line $i+n+1$ gives $x_i$ and $y_i$, representing the $i$-th teacher’s checking route.

Output one integer in one line, which is the answer.

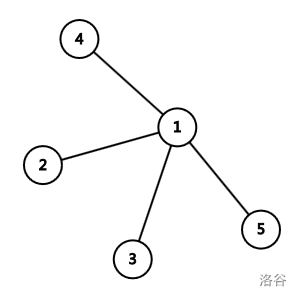
### Sample Explanation #### Sample Explanation $1$  Ysuperman chooses to close the road connecting $1$ and $5$. The teachers’ total dissatisfaction value is $0$. The dormitory is split into $2$ connected components, and the kids’ total dissatisfaction value is $3$. #### Sample Explanation $2$ The graph is the same as in Sample 1. Ysuperman chooses to close the road connecting $1$ and $5$ and also the road connecting $1$ and $4$. The teachers’ total dissatisfaction value is $1$. The dormitory is split into $3$ connected components, and the kids’ total dissatisfaction value is $2$. ------ ### Constraints **This problem uses bundled testdata.** | Subtask | $n$ | $m$ | $k$ | Special Property | Score | |:-:|:-:|:-:|:-:|:-:|:-:| | 1 | $\le 20$ | $\le 10$ | $\le 80$ | None | 8 | | 2 | $\le 150$ | $\le 10^3$ | $\le 8 \times 10^4$ | None | 13 | | 3 | $\le 800$ | $\le 10^5$ | $\le 8 \times 10^7$ | The tree is a chain | 13 | | 4 | $\le 800$ | $\le 10^5$ | $\le 8 \times 10^7$ | The tree is a fully blooming chrysanthemum | 13 | | 5 | $\le 800$ | $\le 10^5$ | $= 0$ | None | 13 | | 6 | $\le 800$ | $\le 10^5$ | $\le 8 \times 10^7$ | None | 40 | [A chain] is defined as: all nodes have degree $\le 2$. [A fully blooming chrysanthemum] is defined as: there exists a node with degree $n-1$. For $100\%$ of the data, it holds that $1 \le h_i \le 10^9$, $0 \le k \le 8 \cdot 10^7$, and $u_i \ne v_i$. Translated by ChatGPT 5