P6601 "EZEC-2" Machine

tlx likes science fiction novels. >In the small universe, only drift bottles and ecological spheres remain. The drift bottles are hidden in the darkness. In a universe of only one thousand square meters, only the little sun inside an ecological sphere emits a faint light. In this tiny world of life, several clear water balls float quietly in a zero-gravity environment. A small fish jumps out of one water ball and into another, lightly swimming among the green algae. In the grass on a small piece of land, a dewdrop detaches from a blade of grass, spins and floats up, refracting a crystal-clear ray of sunlight into space. >$\qquad \qquad \qquad \qquad \qquad \qquad \qquad\qquad\qquad\qquad\qquad\qquad\qquad --$ *The Three-Body Problem* In another universe, it must be another amazing scene. There, gravity seems to have become insignificant, and gravity machines have become commonplace. Inside a gravity machine there is no gravity. That is, if an object moves on the machine, during its movement it is only affected by the gravitational force given by the machine. With some probability, this force makes the object move quickly toward the force-applying object, and when enough momentum is reached, teleportation can be achieved.

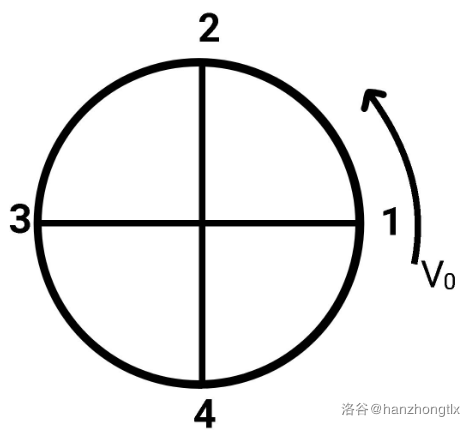
A gravity machine consists of a smooth circular track and $2n$ holes (the holes are numbered counterclockwise from $1$ to $2n$. The measure of the minor arc between every two adjacent holes is $\dfrac{\pi}{n}$). Each hole is connected by a passage to the hole whose angle with it is $\pi$. For example, when $n=2$, hole $1$ is connected to hole $3$. When $n=2$, the structure is roughly like this:  Now we place a ball at hole $1$, making it always move counterclockwise in uniform circular motion. Without teleportation, each second it can move from one hole to the next adjacent hole exactly. Due to the strange structure of the future laboratory (the internal gravity-supplying device is incredible), each time it passes a hole, there is a probability $p$ that it teleports immediately (i.e., without spending time) to the hole on the other side of the passage, and then continues the counterclockwise uniform circular motion. That is, there is a probability $1-p$ that it continues moving along the circle to the next hole. Note that at each unit of time, the ball can teleport at most once. In simple terms, if at some time the ball is at hole $i$, then at the next time it may move to hole $i \bmod 2n + 1$ or $(i + n) \bmod 2n + 1$, with probabilities $1-p$ and $p$, respectively. Now tlx has two identical gravity machines, and two balls start moving from hole $1$ at the same time. He will randomly (all possible choices are equally likely) choose an ordered pair $(i,j)$ $( 1\leqslant i\leqslant 2n,0\leqslant j\leqslant t,i,j\in \mathbb Z )$, representing the hole number and the time, respectively. You need to find the probability that at time $j$, in both gravity machines, hole $i$ simultaneously has a ball staying there (passing through the hole but teleporting to the opposite side does not count as staying). Note: the ball may also teleport to the opposite hole right when it starts moving. For convenience of calculation, we specify that all probabilities are considered modulo $10^9+7$.

The input contains one line with three integers $n,p,t$, representing half the number of holes in the device, the teleportation probability taken modulo $10^9+7$, and the upper bound of the time range for the random choice.

Output one line with one integer, representing the required probability modulo $10^9+7$.

**Constraints and Conventions** **This problem uses bundled testdata.** The scoring is as follows: - Subtask $1$ ($7$ points): $p\in \{0,1\}$. - Subtask $2$ ($13$ points): $t\leqslant 20,n\leqslant50$. - Subtask $3$ ($20$ points): $t\leqslant 10^3,n\leqslant50$. - Subtask $4$ ($10$ points): $t\leqslant 10^3$. - Subtask $5$ ($10$ points): $t\leqslant 10^6$. - Subtask $6$ ($15$ points): $n\leqslant50$. - Subtask $7$ ($25$ points): no special constraints. For $100\%$ of the testdata, $2\leqslant n\leqslant 500$, $0\leqslant p\leqslant 10^9+6$, $0\leqslant t \leqslant 10^9$. **Note: any constraints not explicitly stated are the maximum constraints.** **Sample Explanation #1** $500000004$ is $\dfrac{1}{2}$ modulo $10^9+7$. For convenience below, let $P(i,j)$ be the probability when the chosen ordered pair is $(i,j)$. All ordered pairs with non-zero probability are: $P(1,0)=\dfrac{1}{4},P(3,0)=\dfrac{1}{4},P(2,1)=\dfrac{1}{4},P(4,1)=\dfrac{1}{4}$. All possible ordered pairs are: $(1,0),(1,1),(2,0),(2,1),(3,0),(3,1),(4,0),(4,1)$, a total of $8$ choices. So the total probability is: $$P=\dfrac{1}{8}×\dfrac{1}{4}×4+\dfrac{1}{8}×0×4=\dfrac{1}{8}$$ Modulo $10^9+7$, it is $125000001$, which is the output answer. ------------ **Other Hints** 1. If you do not understand taking fractions modulo, you can see [here](https://www.luogu.com.cn/problem/P2613). 2. If you do not understand how angles are represented in this problem, you can see [radian measure](https://baike.baidu.com/item/弧度制/3315973?fr=aladdin). Translated by ChatGPT 5