P6603 "EZEC-2" Sweet Dream

> Yesterday is no longer today, and hope seems endless. > Separated by life and death, we face two vast emptinesses. > To soothe sorrow and endure longing, the human world is like a dream, > leaning on a smile and riding the cool wind.

There are $n$ dream scenes, with distinct indices in $[1,n]$. PF has schizophrenia, so at the same time he will be in two dreams. **The absolute difference between the indices of the scenes where these two dreams are located must not exceed $l$**. Between scenes there are $m$ **directed** relations. The $i$-th relation connects scenes $u_i$ and $v_i$. There is no scene that is impossible to reach. Each scene has a happiness value. The happiness value of scene $j$ is $a_j$, which is added when the dream passes through it for the **first** time. At the beginning, both dreams are at scene $1$. When both dreams move to scene $n$, PF will wake up. If in some move, the two scenes $A,B$ where PF’s dreams are currently located are both **directly connected** to some scene $C$, then PF can **move both dreams simultaneously** to scene $C$. Otherwise, PF can **only move one dream at a time**. Please write a program to compute the maximum total happiness value that can be obtained when he wakes up.

The first line contains three integers $n,m,l$, representing the number of scenes, the number of relations between scenes, and the maximum allowed distance between PF’s two scenes. The next line contains $n$ integers. The $i$-th number means the happiness value of scene $i$ is $a_i$. The happiness values of scene $1$ and scene $n$ are $0$. The next $m$ lines each contain two integers $u,v(1\le u

If there is a solution, output one integer $q$ in one line, meaning the maximum happiness value obtainable. If there is no solution, output `-1`.

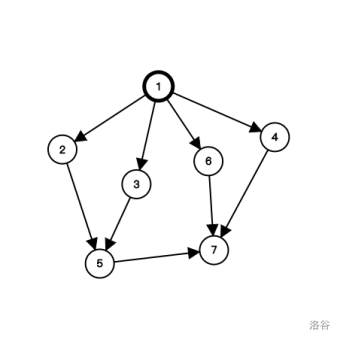
[Large sample](https://www.luogu.com.cn/paste/ar8yuqg6) **[Sample Explanation #1]**  Below, $A,B$ denote the two dreams currently in progress: Move dream $A \space 1 \to 3$, move dream $B \space 1 \to 4$, move dream $A \space 3 \to 5$, then move dreams $A \space B$ simultaneously to scene $7$. The total happiness value is $5+10+10 = 25$. **Note**: If you want to move one dream to scene $6$, then the other dream’s index must be greater than or equal to $4$. However, the only route to $6$ is $1\to 6$, and having scenes $1$ and $4$ at the same time does not satisfy having intermediate scenes $\le l$. Therefore, the only way to pass through scene $6$ is to move both dreams to scene $6$ simultaneously, and the happiness value you can get in that case is $20$. --- **[Constraints and Conventions]** | Test Point ID | $ n \le$ | $ m \le$ | $ l \le$ | $ a_i \le$ | Time | Special Property | | :----------: | :----------: | :----------: | :----------: |:----------: | :----------: |:----------: | | $1,2$ | $10$ | $15$| $5$ | $50$ | $1\text s$ | None | | $3\sim 4$ | $16$ | $40$ | $8$ | $5 \times 10^3$ | $1\text s$ | None | | $5\sim 6$ | $16$ | $120$ | $8$ | $5 \times 10^3$ | $1\text s$ | None | | $7 \sim 10$ | $100$ | $10^3$ | $10$ | $10^4$ | $1 \text s$ | None | | $11$ | $100$ | $10^3$ | $10$ | $10^4$ | $1\text s$ | The scenes form a tree | | $12 \sim 14$ | $10^3$ | $10^4$ | $10$ | $10^4$ | $1\text s$ | None | | $15,16$ | $5\times10^3$ | $3\times10^4$ | $10$ | $10^4$ | $1\text s$ | None | | $17,18$ | $5\times10^3$ | $3\times10^4$ | $11$ | $10^4$ | $2\text s$ | None | | $19,20$ | $5\times10^3$ | $3\times10^4$ | $12$ | $10^4$ | $3\text s$ | None | For $100\%$ of the testdata, $1\le u