P6616 Rings Rings

> In 1929 you do not make a move, in 3949 you walk on the ice, in 5969 you watch the willows across the river; > > In 79 the river opens, in 89 the geese return, in 99 plus one more 9, oxen plow all over the fields. “9” has been a magical number since ancient times, and the problem you need to solve today is also related to “9”.

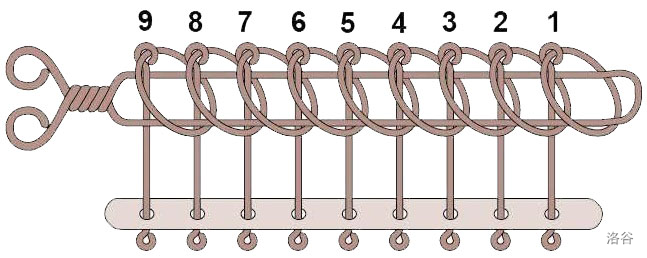
You have an $n$-ring puzzle, which has the same structure as the well-known nine-ring puzzle.  > The figure above shows a nine-ring puzzle. As the name suggests, an $n$-ring puzzle has a long bar, with $n$ rings on it that **affect each other**. We number these $n$ rings: the ring closest to the head of the bar is ring $1$, then ring $2$, and so on; the ring closest to the tail of the bar is ring $n$. Define $f_i$ as the state of ring $i$, where $f_i = 1$ means the ring is on the bar, and $f_i = 0$ means the ring is not on the bar. Define **removing/installing a ring** as **flipping** the ring’s state, i.e. changing the state from $1$ to $0$ or from $0$ to $1$. The legal rules for removing/installing rings are: 1. Ring $1$ can always be removed/installed alone. 2. Ring $k+1$ can be removed/installed alone if and only if $f_k = 1$ and for all $i < k$, we have $f_i = 0$. 3. If $f_1 = f_2$, then rings $1$ and $2$ can be removed/installed together. Now you need to solve the following problem: given the initial state of an $n$-ring puzzle, find the minimum number of legal remove/install operations needed to completely remove the $n$-ring puzzle.

The amount of data in this problem is large, so a **special** input format is used. The first line contains a positive integer $n$. The second line contains a positive integer $m$. The next $m$ lines describe the initial state: Line $i + 2$ contains two integers $len_{i}, st_{i}$, meaning that we continuously append $len_{i}$ rings of state $st_{i}$ to the tail of the initial $n$-ring puzzle.

Output one integer, the minimum number of remove/install operations needed to remove the $n$-ring puzzle starting from the given state. Since the answer may be very large, you only need to output the result modulo $1201201201$.

This problem uses **bundled tests**, with **O2 optimization** enabled. $\text{Subtask 1 (10 pts)}:$ guarantee $1 \le n \le 20$. $\text{Subtask 2 (15 pts)}:$ guarantee $1 \le n \le 1000$. $\text{Subtask 3 (15 pts)}:$ guarantee that there is **only** one $1$ in the initial state. $\text{Subtask 4 (30 pts)}:$ guarantee $1 \le n \le 10^7$. $\text{Subtask 5 (30 pts)}:$ no special constraints. For all testdata, $1 \le n \le 10^{18}$, $1 \le m \le 10^5$, $st_{i} \in \{0, 1\}$, $len_{i} \ge 1$. It is guaranteed that $\sum\limits_{i=1}^m len_{i} = n$. --- #### Sample #1 Explanation The sample describes a $4$-ring puzzle with initial state `1101`. One way to finish with the minimum number of legal remove/install operations is: ```plain 1. 1101 -> 1100 2. 1100 -> 0100 3. 0100 -> 0111 4. 0111 -> 0110 5. 0110 -> 0010 6. 0010 -> 0011 7. 0011 -> 0000 ``` A total of $7$ steps. --- #### Extra Notes In this problem, the 3rd remove/install rule for the $n$-ring puzzle is not mentioned in most nine-ring puzzle instructions, but it is indeed a real and feasible operation. Translated by ChatGPT 5