P6618 Islands Island

> Once there were some islands, and beside the islands there were some bridges. > Bridges connected islands, and islands connected bridges. > > One day, the bridges collapsed and the islands tilted. From then on, bridges had no islands, and islands had no bridges.

In the middle of the vast ocean, there is a huge archipelago system with $n$ islands. For convenience, we number them from island $1$ to island $n$. Among them, island $1$ is the only inhabited island. There are $m$ shaky small bridges among these islands. The $i$-th bridge connects two **different** islands $u_i$ and $v_i$, and **there are no two bridges between the same pair of islands**. The fragile bridges have been abandoned. Each bridge can only be crossed by one person once, and then it will collapse. One day, you suddenly decide to explore this huge archipelago. As an explorer, you know that a safe island exploration route **may visit the same island multiple times**, but it **must never use a collapsed bridge**. An interesting island exploration cycle is a safe island exploration route that **starts and ends at the same island**, and it visits at least two different islands. However, in particular, **in an interesting island exploration cycle, except for the starting island which may be visited twice, every other island may be visited at most once** (obviously, you do not find it interesting to repeatedly visit an island you have already been to). To ensure your safety, you have prepared well and obtained a map of the archipelago. After carefully studying this ancient map, you find that there is at least one way to reach between every pair of islands, and that the $i$-th bridge actually hides a treasure worth $w_i$. However, you also notice that bridges in the archipelago are very scarce, and they always satisfy a rule: **for interesting exploration cycles that start from the same island, any two different cycles will never pass through the same bridge**. You may airdrop onto any island to start your exploration. During the trip, you can collect treasures, but in the end you **must return to island** $1$ in order to return safely. Now, you want to know the maximum total value of treasures you can collect **while ensuring your safety**. 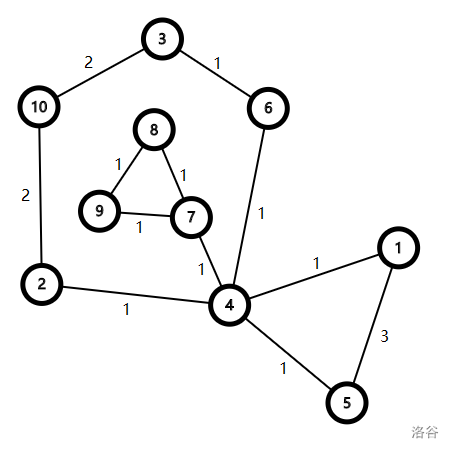--- #### Explanation for Sample #1  > Above is the map of the archipelago. Circles represent islands, and the lines between circles represent bridges. > > The number inside each circle is the island index, and the number next to each line is the value of the treasure on that bridge.  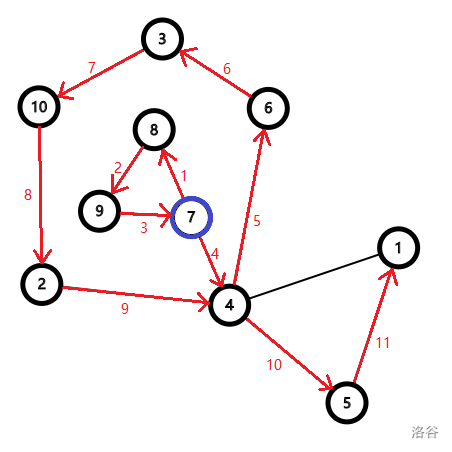Start from island $7$, follow the direction and order shown in the figure above, and the total value of collected treasures is $15$, which is the answer.

The first line contains two positive integers $n, m$, representing the number of islands and the total number of bridges connecting islands. The next $m$ lines each contain three positive integers. The $i$-th line contains $u_i, v_i, w_i$, with meanings as described above.

Output one integer in a single line, representing the maximum total value of treasures you can collect **while ensuring your safety**.

This problem uses **bundled testdata**, with **O2 optimization** enabled. $\text{Subtask 1 (3 pts)}:$ It is guaranteed that there are no interesting exploration cycles. $\text{Subtask 2 (7 pts)}:$ It is guaranteed that $1 \le n \le 10$. $\text{Subtask 3 (10 pts)}:$ It is guaranteed that no two interesting exploration cycles pass through the same island. $\text{Subtask 4 (10 pts)}:$ It is guaranteed that $w_i = 1$. $\text{Subtask 5 (20 pts)}:$ It is guaranteed that $1 \le n \le 2000$. $\text{Subtask 6 (20 pts)}:$ It is guaranteed that $1 \le n \le 10^5$. $\text{Subtask 7 (30 pts)}:$ No special constraints. For all data, $1 \le n \le 3\times10^5$, $1 \le m \le10^6$, and $1 \le w_i \le 10^9$. Translated by ChatGPT 5