P6635 「JYLOI Round 1」箭头调度

moyu_028 给了你一个有 $n$ 个点 $m$ 条边的无向图，现在要给每条边赋一个方向，现在请你求出一个赋方向的方案，使得按照这个方案能够生成一个拓扑序，且使得这个拓扑序是在所有可能的拓扑序中字典序第 $k$ 小的。

输入的第 1 行有 3 个正整数 $n$、$m$、$k$，含义如题所述。 接下来有 $m$ 行，这 $m$ 行中的第 $i$ 行有两个正整数 $x_i$ 和 $y_i$，表示有一条从 $x_i$ 到 $y_i$ 的无向边。

输出为一行一个长度为 $m$ 的 01 串，这个 01 串中的第 $i$ 个字符表示从 $x_i$ 和 $y_i$ 之间的无向边的方向，为 0 则表示这条边是从 $x_i$ 到 $y_i$，为 1 则表示这条边是从 $y_i$ 到 $x_i$。可以证明答案唯一，且数据保证有解。

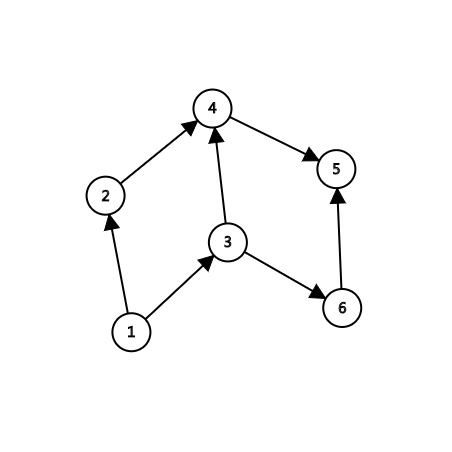
## 提示 拓扑序：在一个 DAG（有向无环图）中，我们将图中的顶点以线性方式进行排序，使得对于任何的顶点 $u$ 到 $v$ 的有向边 $(u,v)$，都可以有 $u$ 在 $v$ 的前面，则这样的序列称为拓扑序。 ---------- ## 样例解释 ### 样例 1 解释 答案的图如下，根据图可得出答案。  ----------------- ## 数据范围 对于 $100\%$ 的数据，$1 \leq n \leq 11, 1 \leq m \leq 2 \times 10^3, 1 \leq k \leq 10^8，1 \leq x_i, y_i \leq n, x_i \not= y_i$。 对于测试点 1（10 分）：$n = 1$。 对于测试点 2（30 分）：$n \leq 11, m \leq 20$。 对于测试点 3（30 分）：$n \leq 11, k = 1$。 对于测试点 4（30 分）：无特殊限制。 本题共 4 个测试点，总分为 100 分，单个测试点的时间限制为 5 秒。 ## 题目来源 「JYLOI Round 1」 A Idea：moyu_028 & abcdeffa Solution：LiuXiangle Data：abcdeffa