P6643 [CCO 2020] Mountains and Valleys

There is an undirected graph with $N$ vertices and $M$ edges, and each edge has a weight. The graph has no multiple edges and no self-loops. The vertices are numbered starting from $0$. Exactly $N - 1$ edges have weight $1$. All other edges have weight $\ge \left\lceil \frac{N}{3} \right\rceil$ and $\le N$. Also, if we only consider the edges with weight $1$, the whole graph forms a tree. Now you need to traverse every vertex exactly once, while making the total weight of the edges you travel as small as possible. Find the minimum possible total edge weight. **Reminder:** - You may go back and forth along an edge. - You may choose any vertex to start from. - You have only one person.

The first line contains two integers $N, M$. The next $M$ lines each contain three integers $x_i, y_i, w_i$, indicating that there is an edge between $x_i$ and $y_i$ with weight $w_i$.

Output the minimum total edge weight required to traverse every vertex exactly once.

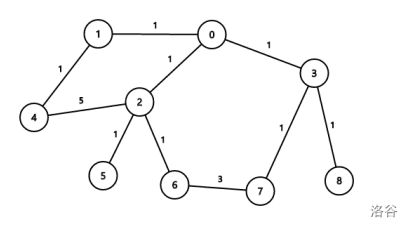
#### Sample Explanation  An optimal path is $4\to 1\to 0\to 2\to 5\to 2\to 6\to 7\to 3\to 8$, with total edge weight $1+1+1+1+1+1+3+1+1=11$. #### Subtasks **This problem uses bundled testdata.** - Subtask 1 ($4$ points): $N\le 6$, $M\le 10$. - Subtask 2 ($8$ points): $N\le 20$, $M\le 40$. - Subtask 3 ($8$ points): $N\le 5\times 10^3$, $M\le 10^5$, and $w_i=1$ or $\left\lceil\frac{N}{2}\right\rceil\le w_i\le N$. - Subtask 4 ($24$ points): $N\le 100$, $M\le 200$. - Subtask 5 ($8$ points): $N\le 500$, $M\le 10^3$. - Subtask 6 ($12$ points): $N\le 5\times 10^3$, $M\le 10^4$. - Subtask 7 ($20$ points): $N\le 8\times 10^4$, $M\le 1.6\times 10^5$. - Subtask 8 ($16$ points): No special restrictions. For $100\%$ of the data, it is guaranteed that $4\le N\le 5\times 10^5$, $N-1 \le M\le 2\times 10^6$, $0\le x_i,y_i\le N-1$, and $w_i=1$ or $\left\lceil \frac{N}{3}\right\rceil\le w_i\le N$. #### Notes This problem is translated from [Canadian Computing Olympiad 2020](https://cemc.math.uwaterloo.ca/contests/computing/2020/index.html) [Day 1](https://cemc.math.uwaterloo.ca/contests/computing/2020/cco/day1.pdf) T3 Mountains and Valleys。 Translated by ChatGPT 5