P6643 [CCO 2020] Mountains and Valleys

有一个有 $N$ 个点 $M$ 条边，边有边权的无向图，图无重边、无自环，点的标号从 $0$ 开始。 共有 $N-1$ 条边的边权为 $1$，其余边的边权均 $\ge \lceil \frac{N}{3} \rceil$ 且 $\le N$，同时，如果仅考虑边权为 $1$ 的边，整个图会是一棵树。 现在您要遍历每个点一遍，且使经过的边权总和最小。 求最小的边权总和。 **提醒：** - 您可以往返走一条边。 - 您可以任选一个点出发。 - 您只有一个人。

第一行为两个整数 $N,M$。 接下来 $M$ 行，一行三个整数 $x_i,y_i,w_i$，表示有一条从 $x_i$ 到 $y_i$，边权为 $w_i$ 的边。

遍历每个点一遍，所需最小的边权总和。

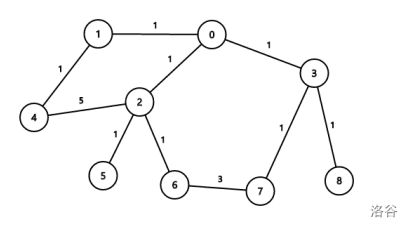
#### 样例解释  最优路径为 $4\to 1\to 0\to 2\to 5\to 2\to 6\to 7\to 3\to 8$，边权和为 $1+1+1+1+1+1+3+1+1=11$。 #### 子任务 **本题使用捆绑测试。** - Subtask 1（$4$ 分）：保证 $N\le 6$，$M\le 10$。 - Subtask 2（$8$ 分）：保证 $N\le 20$，$M\le 40$。 - Subtask 3（$8$ 分）：保证 $N\le 5\times 10^3$，$M\le 10^5$，$w_i=1$ 或 $\lceil\frac{N}{2}\rceil\le w_i\le N$。 - Subtask 4（$24$ 分）：保证 $N\le 100$，$M\le 200$。 - Subtask 5（$8$ 分）：保证 $N\le 500$，$M\le 10^3$。 - Subtask 6（$12$ 分）：保证 $N\le 5\times 10^3$，$M\le 10^4$。 - Subtask 7（$20$ 分）：保证 $N\le 8\times 10^4$，$M\le 1.6\times 10^5$。 - Subtask 8（$16$ 分）：无特殊限制。 对于 $100\%$ 的数据，保证 $4\le N\le 5\times 10^5$，$N-1 \le M\le 2\times 10^6$，$0\le x_i,y_i\le N-1$，$w_i=1$ 或者 $\lceil \frac{N}{3}\rceil\le w_i\le N$。 #### 说明 本题译自 [Canadian Computing Olympiad 2020](https://cemc.math.uwaterloo.ca/contests/computing/2020/index.html) [Day 1](https://cemc.math.uwaterloo.ca/contests/computing/2020/cco/day1.pdf) T3 Mountains and Valleys。