P6653 [YsOI2020] Afforestation.

“Continuing from before.” In response to the call, Ysuperman decided to plant a forest outside the kindergarten. Well, if that is the case, Ysuperman will be able to play games with the kids in this hot summer.

To carry out environmental protection work, Ysuperman bought a batch of trees, and they all look the same. Since the trees have not been planted yet, they do not have roots, so they can be considered **unrooted trees**. Ysuperman thinks it is too boring to plant trees that all look the same, so they asked a gardening company to plan it. The gardening company provided a method—“grafting”. The definition of the “grafting” operation is given below: Define a “leaf node” as a node in the tree with degree $1$. A “grafting” operation means: adding a new “leaf node” to an **unrooted tree**. 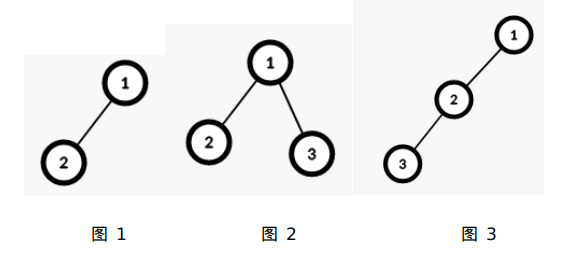For example:  Figure 2 is the tree obtained by performing one valid grafting operation on the tree in Figure 1, and Figure 3 is also a tree obtained by performing one valid grafting operation on the tree in Figure 1. Also, we know that a tree has a basic property: “species”. The “species” of a tree is the **multiset formed by the maximum subtree size of each node**. Two trees have different “species” if and only if the **multisets formed by the maximum subtree size of each node are different**. Here, the **maximum subtree size** of a node means: after deleting this node, the **number of nodes contained in the largest connected component**. 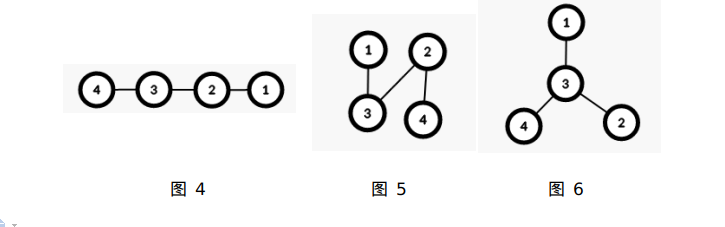For example:  The multiset formed by the maximum subtree size of each node in the tree in Figure 4 is: $ \{ 2,2,3,3 \} $ The multiset formed by the maximum subtree size of each node in the tree in Figure 5 is: $ \{ 2,2,3,3 \} $ The multiset formed by the maximum subtree size of each node in the tree in Figure 6 is: $ \{ 1,3,3,3 \} $ So, the tree in Figure 4 has the same “species” as the tree in Figure 5, and a different “species” from the tree in Figure 6. Ysuperman wants to know: with exactly one “grafting” operation, how many different “species” of trees can be constructed, and for each “species”, how many different “grafting” methods can construct it. Please output, **from small to large**, the number of “grafting” methods for each “species”. Two “grafting” plans are different if and only if, in the “grafting” operation, the node directly connected to the newly added “leaf node” is different.

The first line contains an integer $n$. The next $n-1$ lines each contain two integers $u,v$, indicating that there is an **undirected edge** between $u$ and $v$.

The first line contains an integer $cnt$, indicating how many different “species” of trees can be constructed. From the second line to the $(cnt+1)$-th line, output, **from small to large**, the number of “grafting” methods for each “species”.

**This problem uses bundled tests.** ### Sample Explanation 1 It is possible to construct $1$ kind of tree with “species” $\{2,4,4,5,5,5\}$. It is possible to construct $2$ kinds of trees with “species” $\{3,3,4,5,5,5\}$. It is possible to construct $2$ kinds of trees with “species” $\{3,3,4,4,5,5\}$. ### Sample Explanation 2 It is possible to construct $1$ kind of tree with “species” $\{3,5,5,7,7,7,7,7\}$. It is possible to construct $2$ kinds of trees with “species” $\{4,4,5,7,7,7,7,7\}$. It is possible to construct $4$ kinds of trees with “species” $\{4,4,5,6,7,7,7,7\}$. For $100\%$ of the data, $1 \le n\le2\cdot 10^6$. Define a “path” as a tree in which all nodes have degree at most $2$. Define a “star” as a tree that contains $n-1$ “leaf nodes”. Special Property 1: The shape of the tree is guaranteed to be a “path”. Special Property 2: The shape of the tree is guaranteed to be a “star”. Special Property 3: The shape of the tree is guaranteed to be a complete binary tree. | subtask | $n$ | Special Property | Score | Time Limit | | :-----------: | :-----------: | :-----------: | :--------:| :---------:| | 1 | $\le 2\cdot 10^6$ | 2 | 2 | 4s | | 2 | $\le 2\cdot 10^6$ | 1 | 3 | 4s | | 3 | $\le 300$ | None | 5 | 1s | | 4 | $\le 2\cdot10^6$ | 3 | 7 | 4s | | 5 | $\le 5000$ | None | 23 | 1s | | 6 | $\le 5\cdot10^4$ | None | 29 | 2s | | 7 | $\le 2\cdot10^6$ | None | 31 | 4s | ### Notes If you do not know what a complete binary tree means, Ysuperman provides a link: [Link](https://zh.wikipedia.org/zh/%E4%BA%8C%E5%8F%89%E6%A0%91#%E5%AE%8C%E5%85%A8%E4%BA%8C%E5%8F%89%E6%A0%91). The input and output are large, so please use a fast I/O method. If you use a recursive algorithm that requires a large amount of stack space, you can first run ```sudo su``` locally (under NOI linux) to get permission, and then use the command ```ulimit -s unlimited ``` to enable an unlimited stack. The problem is not difficult. Translated by ChatGPT 5