P6658 边三连通分量

对于一张无向图 $G = (V, E)$。 - 我们称两个点 $u, v ~ (u, v \in V, u \neq v)$ 是边三连通的，当且仅当存在三条从 $u$ 出发到达 $v$ 的，相互没有公共边的路径。 - 我们称一个点集 $U ~ (U \subseteq V)$ 是边三连通分量，当且仅当对于任意两个点 $u', v' ~ (u', v' \in U, u' \neq v')$ 都是边三连通的。 - 我们称一个边三连通分量 $S$ 是极大边三连通分量，当且仅当不存在 $u \not \in S$ 且 $u \in V$，使得 $S \cup \{u\}$ 也是边三连通分量。

给出一个 $n$ 个点，$m$ 条边的无向图 $G = (V, E)$，$V = \{1, 2, \ldots, n\}$，请求出其所有的极大边三连通分量。

第一行输入两个整数 $n, m$，表示点数、边数。 接下来 $m$ 行，每行输入两个数 $u, v$，表示图上的一条边。

第一行输出一个整数 $s$，表示极大边三连通分量个数。 接下来输出 $s$ 行，每行若干整数，表示一个极大边三连通分量内所有点。 对于单个极大边三连通分量，请将点按照标号升序输出。对于所有极大边三连通分量，请按照点集内编号最小的点升序输出。

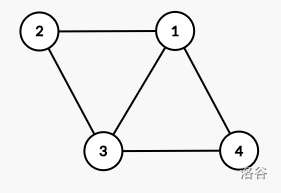
#### 样例 1 解释  如图，$1 \to 3$ 共有 $(1, 2, 3)$，$(1, 3)$，$(1, 4, 3)$ 三条路径，它们互相都没有相交的边。因此 $1$ 与 $3$ 在同一个边三连通分量中。 由于 $2$，$4$ 点度都只有 $2$，不可能有三条边不相交的到其它点的路径，因此它们自己形成边三联通分量。 --- #### 数据范围 - 对于 $30\%$ 的数据，$n \le 100$，$m \le 200$。 - 对于 $50\%$ 的数据，$n \le 1000$，$m \le 2000$。 - 对于 $80\%$ 的数据，$n \le 10 ^ 5$，$m \le 2 \times 10 ^ 5$。 - 对于 $100\%$ 的数据，$1 \le n, m \le 5 \times 10 ^ 5$，$1 \le u, v \le n$。可能有重边和自环。 --- #### 来源 题目搬运自 [Three-Edge-Connected Components](https://judge.yosupo.jp/problem/three_edge_connected_components)。