P6676 [COCI 2019/2020 #2] Slagalica

## 本题征集 SPJ。但若您写的是正解，即，输出了字典序最小解，仍可获得 AC 的评测结果。 小斌喜欢玩拼图。

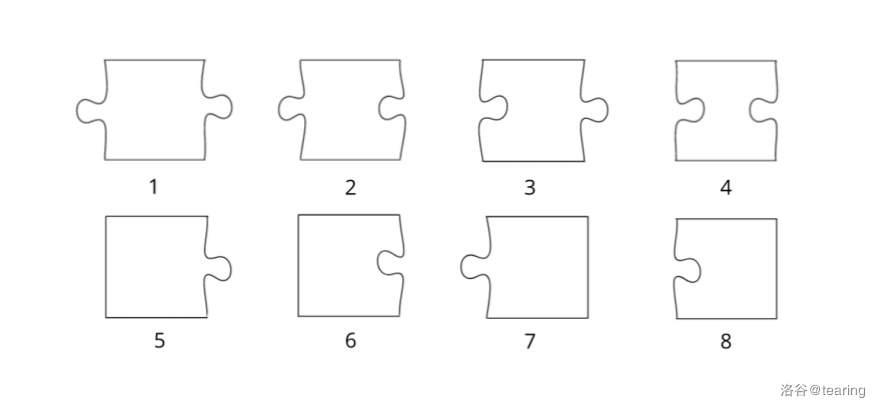
小斌得到了一个由 $n$ 个部分组成的一维拼图游戏。他很快意识到每块拼图都属于以下类型之一：  另外，已知在这 $n$ 片拼图中，恰好有一个 $5$ 号拼图或 $6$ 号拼图（左边框）和一个 $7$ 号拼图或 $8$ 号拼图（右边框）。 小斌希望将所有块排列成一行，以使第一个（最左边的）拼图类型为 $5$ 号拼图或 $6$ 号拼图，而最后一个（最右边的）拼图类型为 $7$ 号拼图或 $8$ 号拼图。如果有两块拼图，则可以彼此相邻放置，并且仅当它们的相邻边框的形状不同时，即一个边框具有凹凸，而另一个边框具有一个凸出才可以相邻放置。 对于小斌来说，这个问题太简单了，因此他决定在每个部分上写一个唯一的正整数。现在，他想要寻找出字典序最小的方案。 注意：拼图不能旋转！

输入数据共 $n + 1$ 行。 第一行，一个正整数 $n$。 接下来，$n$ 行，包含两个整数 $x_i$ 和 $a_i$，它们表示 $i$ 的类型，$x_i$ 拼图编号，$a_i$ 表示 Fabian 在上面写的数字。数据保证所有 $a_i$ 不重复。

输出数据共一行。 第一行，如果小斌无法解决拼图游戏，输出 `-1`。 否则，您应该输出拼图上数字按字典序排列最小的方案。

#### 样例 #1 解释 只有 $2$ 种解法，如下：  可以看出，第二种解法的字典序较小，所以输出 `1 3 7 5 4`。 #### 数据规模及约定 对于 $100\%$ 的数据，$2 \le n \le 10^5, 1 \le x_i \le 8, 1 \le a_i \le 10^9$。 没有给出字典序最小解而只构造一组解可以得到 $40\%$ 的分数。 #### 说明 **本题分值按 COCI 原题设置，满分 $70$。** **题目译自 [COCI2019-2020](https://hsin.hr/coci/archive/2019_2020/) [CONTEST #2](https://hsin.hr/coci/archive/2019_2020/contest2_tasks.pdf) *T2 Slagalica*。**