P6692 Spawn Point.

Little L, Little W, and Little H are playing a van♂ game together. ~~Since Little L is too bad, he ends up just watching Little W and Little H play the game all the time.~~

The map of this game can be abstracted as a grid with $n$ rows and $m$ columns. There are $k$ obstacle cells on the grid, and the edge length between two adjacent cells is $1$. When the game starts, ~~Little L~~ Little W and Little H will **each** randomly spawn at a cell. Of course, they **will not spawn on obstacle cells**. Little L, who ~~often dies at the start~~, watches the paths that Little W and Little H take to meet up each time, and wants to know the expected distance between them after they spawn each time. (Here, the distance means the [Manhattan distance](https://www.luogu.com.cn/blog/xuxing/Distance-Algorithm) between two points, i.e., $\left|x_1-x_2\right|+\left|y_1-y_2\right|$.) Since Little L can easily compute how many spawn arrangements there are, you actually **only need to tell him the sum of the distances between them over all cases**. **Note**: The case where Little W spawns at point $A$ and Little H spawns at point $B$, and the case where Little W spawns at point $B$ and Little H spawns at point $A$, are considered **the same case**.

The first line contains three integers $n,m,k$, representing the number of rows, the number of columns, and the number of obstacle cells. The next $k$ lines each contain two positive integers $x_i,y_i$, representing the position of the $i$-th obstacle.

Output one integer, representing **the sum of the distances between Little W and Little H’s spawn points over all cases**. Since Little L is extremely bored, he asks you to output the answer modulo $10^9+7$.

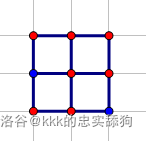
For sample 1, the map looks like this (blue points are obstacles, red points are possible spawn points):  + Spawn points are $(1,1)$ and $(1,1)$, distance is $0$. + Spawn points are $(1,1)$ and $(1,2)$, distance is $1$. + Spawn points are $(1,1)$ and $(1,3)$, distance is $2$. + Spawn points are $(1,1)$ and $(2,2)$, distance is $2$. + Spawn points are $(1,1)$ and $(2,3)$, distance is $3$. + Spawn points are $(1,1)$ and $(3,1)$, distance is $2$. + Spawn points are $(1,1)$ and $(3,2)$, distance is $3$. + Spawn points are $(1,2)$ and $(1,2)$, distance is $0$. + Spawn points are $(1,2)$ and $(1,3)$, distance is $1$. + Spawn points are $(1,2)$ and $(2,2)$, distance is $1$. + Spawn points are $(1,2)$ and $(2,3)$, distance is $2$. + Spawn points are $(1,2)$ and $(3,1)$, distance is $3$. + Spawn points are $(1,2)$ and $(3,2)$, distance is $2$. + Spawn points are $(1,3)$ and $(1,3)$, distance is $0$. + Spawn points are $(1,3)$ and $(2,2)$, distance is $2$. + Spawn points are $(1,3)$ and $(2,3)$, distance is $1$. + Spawn points are $(1,3)$ and $(3,1)$, distance is $4$. + Spawn points are $(1,3)$ and $(3,2)$, distance is $3$. + Spawn points are $(2,2)$ and $(2,2)$, distance is $0$. + Spawn points are $(2,2)$ and $(2,3)$, distance is $1$. + Spawn points are $(2,2)$ and $(3,1)$, distance is $2$. + Spawn points are $(2,2)$ and $(3,2)$, distance is $1$. + Spawn points are $(2,3)$ and $(2,3)$, distance is $0$. + Spawn points are $(2,3)$ and $(3,1)$, distance is $3$. + Spawn points are $(2,3)$ and $(3,2)$, distance is $2$. + Spawn points are $(3,1)$ and $(3,1)$, distance is $0$. + Spawn points are $(3,1)$ and $(3,2)$, distance is $1$. + Spawn points are $(3,2)$ and $(3,2)$, distance is $0$. The total sum is $42$. ### Constraints **This problem uses bundled testdata.** + Subtask 1 ( $10\%$ ): $n,m\leq 80$. + Subtask 2 ( $20\%$ ): $n,m\leq 5000$. + Subtask 3 ( $15\%$ ): $k=0$. + Subtask 4 ( $15\%$ ): $m=1$. + Subtask 5 ( $40\%$ ): no special restrictions. For $100\%$ of the data, $1\leq n,m\leq 10^9,1\leq x_i\leq n,1\leq y_i\leq m,0\leq k\leq 5\times 10^5,k