强迫症

小 L 是一个严重的强迫症患者。 由于他严重的强迫症，所以他画图时总是要把点画在一个圆上。

一天，他问了小 H 和小 W 这样一个问题： 如果在一个圆上有 $n$ 个不同的点，依次标号为 $1$ 到 $n$，有多少种方案能把它们连成一棵树？ 小 H & 小 W：这不是sb题吗？ 小 L：那如果**连边不能相交**呢？ 小 H & 小 W：这不是sb题吗？ 小 L：那如果把「树」换成「图」呢呢？ 小 H & 小 W：这不是sb题吗？ 小 L：那如果给每个点一个权值 $a_i$，连接 $(i,j)$ 的边权值为 $a_i\times a_j$，求**满足上面**的图的**期望所有边权值之和**呢？ 小 H & 小 W：这不是sb题吗？ 小 L 见自己辛苦做了许久都没写出的题目被 dalao 轻松秒杀后十分郁闷。为了安慰他，你需要帮他做出这个问题。 **注意**： 1. 两条边在端点处**不视作相交**。 1. **没有边的图（即只有 $n$ 个点，之间没有边相连）也合法** 1. 点**按顺时针从 $1$ 到 $n$** 编号。 1. 图中**不能有自环和重边**

第一行一个正整数 $n$，意义如上。 接下来一行 $n$ 个非负整数，第 $i$ 个数为 $a_i$，表示第 $i$ 个点的点权。

一个正整数，表示结果。答案对 $998244353$ 取模。

4
1 1 1 1

665496238

13
1 1 4 5 1 4 1 9 1 9 8 1 0

748867567

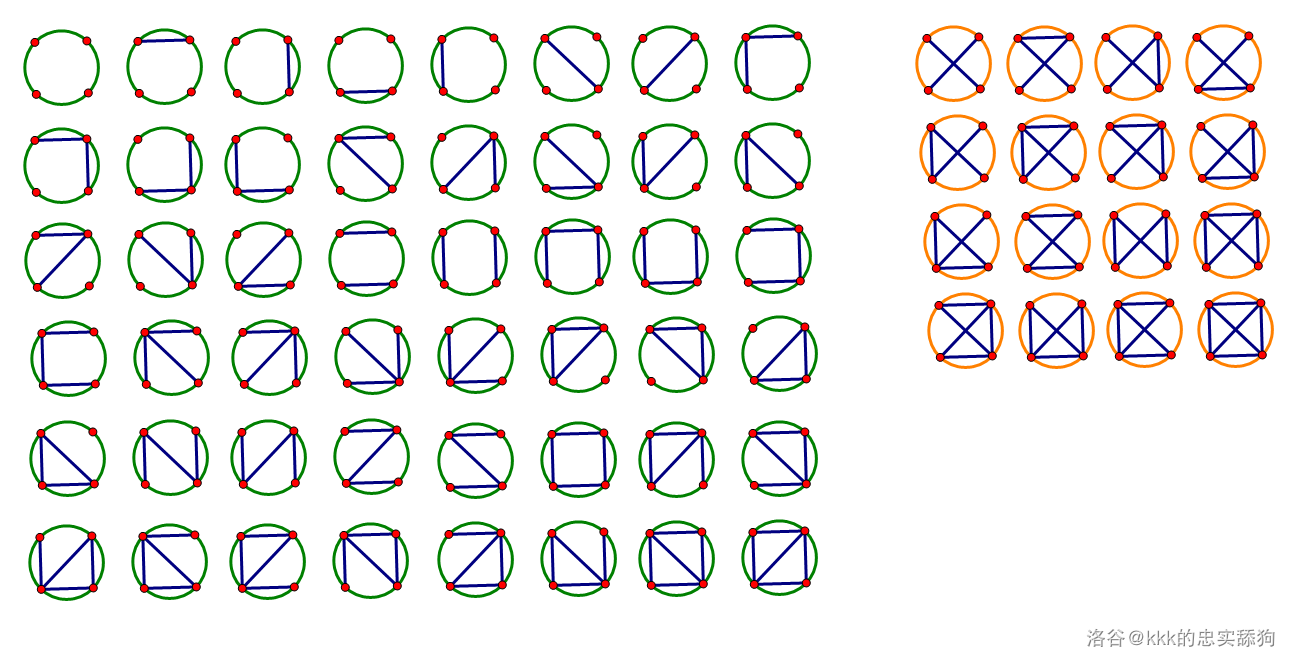
对于样例一，全部 $64$ 张图如下：  其中左侧 $48$ 张图合法，右侧 $16$ 张图不合法，所有边的权值均为 $1$。 期望边权和为 $\dfrac{8}{3}$，模 $998244353$ 意义下结果为 $665496238$。 ### 数据范围 **本题采用捆绑测试。** - Subtask 1( $10\%$ )：$n\leq 6$。 - Subtask 2( $30\%$ )：$n\leq 3000$。 - Subtask 3( $60\%$ )：无特殊限制。 对于 $100\%$ 的数据，$2\leq n\leq 10^5,0\leq a_i\leq10^6$。 Subtask 1 和 Subtask 2 时限 $1s$，Subtask 3 时限 $2s$。 ------------ 如果你不知道如何对一个有理数取模，请自行百度「乘法逆元」