P6719 [BalkanOI 2011] 2circles
题目描述
在平面直角坐标系上有一个含 $N$ 个点的凸多边形,现在想在里面放入两个半径为 $R$ 的圆,使两个圆不重合,求 $R$ 的最大值。
输入格式
第一行为一个整数 $N$。
接下来 $N$ 行,一行两个整数 $x_i,y_i$,表示该多边形第 $i$ 个点的坐标。
输出格式
仅一个实数 $R$。
说明/提示
#### 样例 1 解释
将两个圆心放在该正方形的对角线上的时候,半径最长,如图:
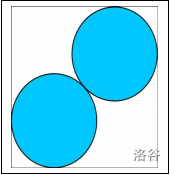
半径为 $\frac{\sqrt{2}}{2\times (1+\sqrt{2})}\approx 0.293$。
#### SPJ 计分标准
若您的答案与标准答案误差不超过 $0.001$,您就会 AC。
#### 数据范围及限制
- 对于 $10\%$ 的数据,保证 $N=3$。
- 对于 $40\%$ 的数据,保证 $N\le 250$。
- 对于 $100\%$ 的数据,保证 $3\le N\le 5\times 10^4$,$-10^7\le x_i,y_i\le 10^7$,这些点按逆时针方向给出。
#### 说明
本题译自 [Balkan Olympiad in Informatics 2011](http://www.boi2011.ro/boi2011/) [Day 1](http://www.boi2011.ro/boi2011/?pagina=probleme) [T1 2circles](http://www.boi2011.ro/resurse/tasks/2circles.pdf)。