P6722 "MCOI-01" Village

Today, the kind and lovely 0x3 Miaojang rode a little pony to a village. “Eh, the layout of this village...” “Feels like the place where I played Ciste before, qwq.” 0x3 Miaojang has a map that contains information about this village. Then 0x3 Miaojang wants to use this map to determine whether Ciste has a solution or not. Note: Ciste is a treasure-map game in *Is the Order a Rabbit?*.

The village is simplified into an undirected connected graph with $n$ nodes (numbered from $1$ to $n$) and $n-1$ edges. 0x3 Miaojang thinks the information in this undirected graph is related to a new graph that satisfies the following conditions: - The vertex set of the new graph is the same as that of the original graph. - In the new graph, there is an undirected edge between $u$ and $v$ if and only if $dis(u,v) \ge k$ in the original graph ($k$ is a given constant, and $dis(u,v)$ is the length of the shortest path from node $u$ to node $v$). 0x3 Miaojang also believes that if this "new graph" is a bipartite graph, then Ciste "has a solution"; if this "new graph" is not a bipartite graph, then this Ciste "has no solution". (If you do not know what a bipartite graph is, please see the Hint.) So 0x3 Miaojang would like you to determine whether this Ciste "has a solution".

The first line contains a positive integer $T$, meaning there are $T$ test cases. For each test case, the first line contains two positive integers $n,k$. Then follow $n-1$ lines, each containing three positive integers $x,y,v$, meaning there is an undirected edge of weight $v$ between node $x$ and node $y$. The input is guaranteed to be valid.

For each test case, output one line: if it "has a solution", output `Yes`, otherwise output `Baka Chino`.

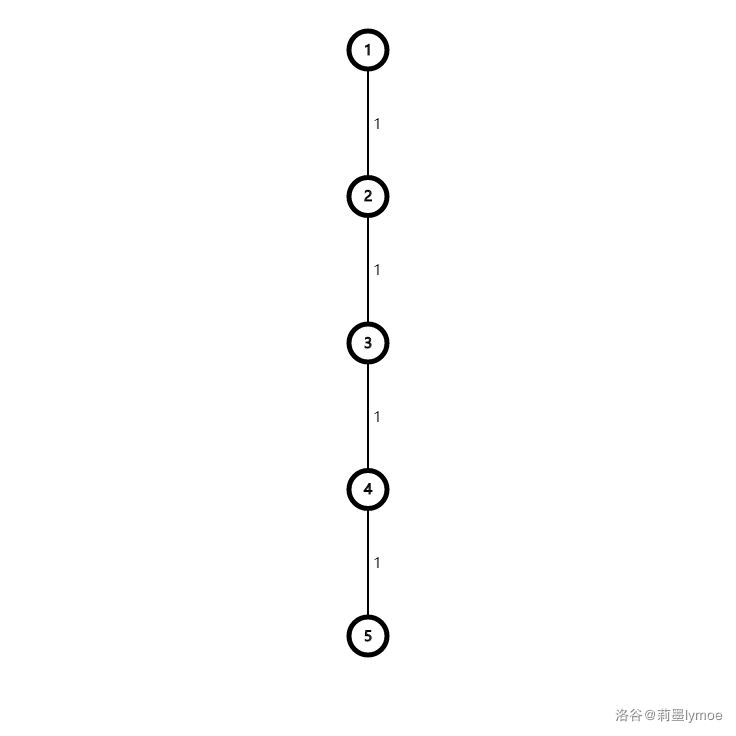
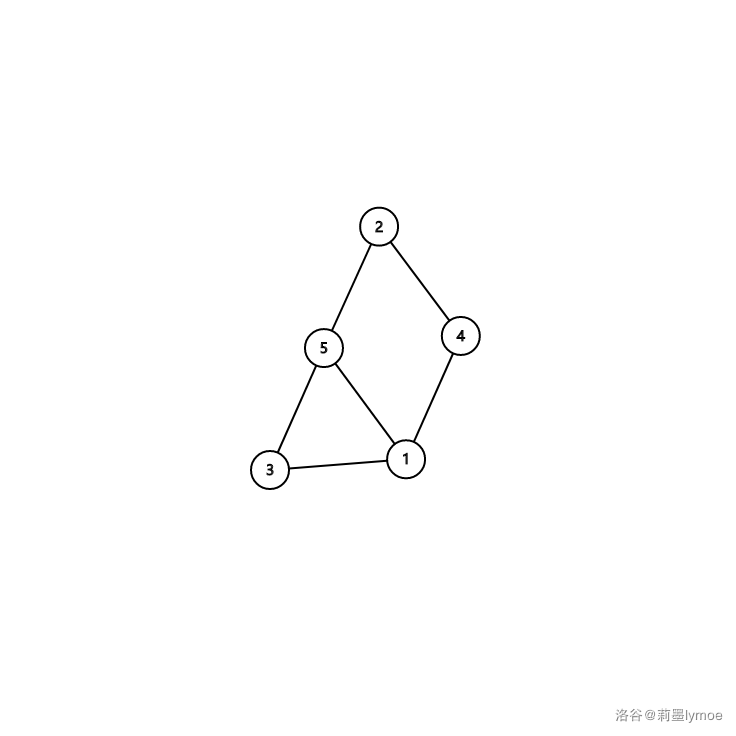
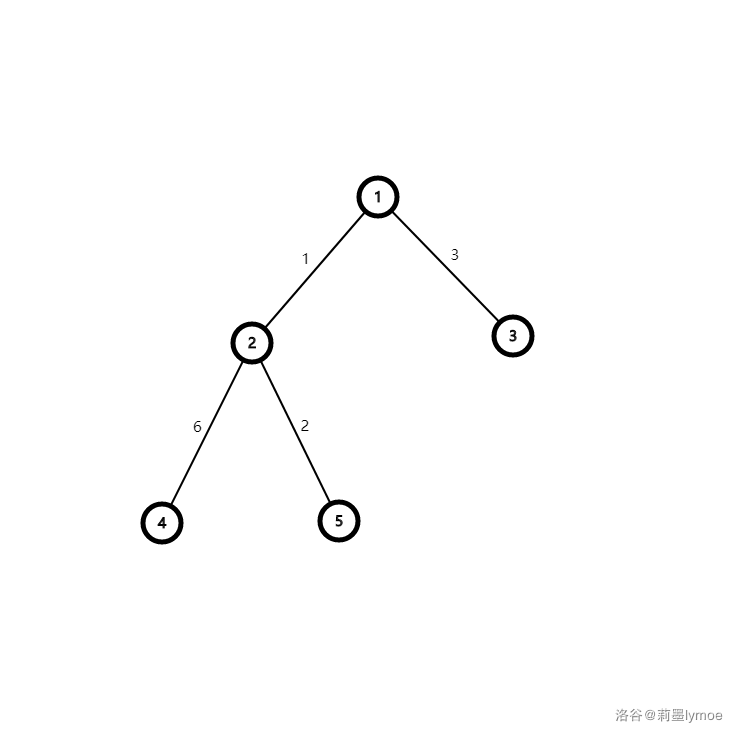
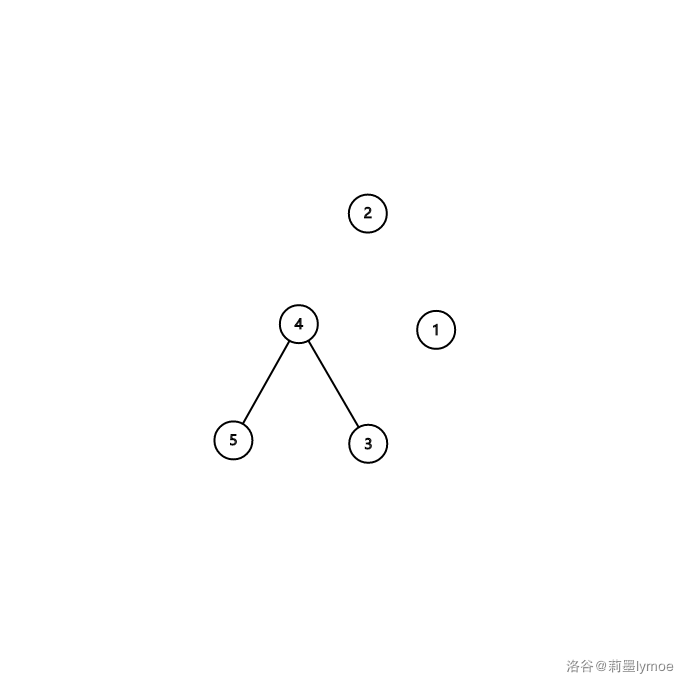
#### Sample Explanation For the **first** test case in the samples: Original graph:  New graph:  The new graph is not bipartite, so output `Baka Chino`. For the **third** test case in the samples: Original graph:  New graph:  The new graph is bipartite, so output `Yes`. #### Constraints **This problem uses bundled testdata**. - Subtask 1 (16 pts): $n \le 10$. - Subtask 2 (24 pts): $n \le 100$. - Subtask 3 (8 pts): $n \le 1000$. - Subtask 4 (28 pts): the graph degenerates into a chain. - Subtask 5 (24 pts): no special restrictions. For $100\%$ of the testdata, $n \le 10^5$, $T \le 10$, $v \le 1000$, $k \le 1000000$. The testdata of this problem is generated using [CYaRon](https://www.luogu.org/discuss/show?postid=11410). #### Hint A **bipartite graph** (also called a bipartite graph / "erbufen tu") is a special model in graph theory. Let $G=(V,E)$ be an undirected graph. If the vertex set $V$ can be divided into two disjoint subsets $(A,B)$, and every edge $(i,j)$ in the graph connects two vertices $i$ and $j$ that belong to these two different sets respectively $(i \in A,j \in B)$, then the graph $G$ is called a bipartite graph. (Quoted from [Baidu Baike](https://baike.baidu.com/item/%E4%BA%8C%E5%88%86%E5%9B%BE/9089095?fr=aladdin).) #### Notes Minecraft OI Round 1 A - Idea: 0x3 Miaojang. - Solution/Std: 0x3 Miaojang. - Data: 0x3 Miaojang. - Tester: tarjin. Translated by ChatGPT 5