P6726 [COCI 2015/2016 #5] POPLAVA
题目描述
有一个由 $N$ 列组成的柱状图,从左至右的柱子高度分别为 $h_1,h_2,\dots,h_N$。
现在你需要向其中储水,柱状图的容量定义为使得水的结构“稳定”时最多所能储水的量。即水在重力作用下不会流动。下图为一个稳定的例子。
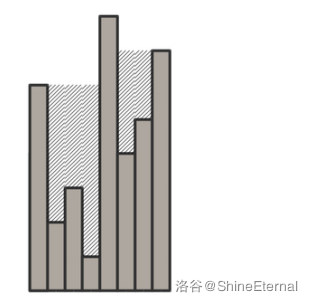
具体来说,我们设从左至右每一列上水的高度为 $v_1,v_2,\dots,v_N$。记 $s_i=h_i+v_i$ ,当满足下列条件时为稳定状态:
- 对于任意的 $i\geq2$,当$v_i>0$ 时,有$s_i\le s_{i-1}$;
- 对于任意的 $i\le N-1$,当$v_i>0$ 时,有$s_i\le s_{i+1}$;
- $v_1=v_N=0$。
现在你需要选择一个 $1\sim N$ 的排列作为柱子 $h_1,h_2,\dots,h_N$ 的高度,使得柱状图的容量为 $X$。如果不存在,则输出 `-1`。如果有多种方案,输出任意一种即可。
输入格式
输入一行两个整数 $N,X$。
输出格式
如果方案不存在,输出 `-1`;
否则输出一行 $N$个整数,为 $h_1,h_2,\dots,h_N$。**输出任意一种方案即可,本题使用 SPJ。**
说明/提示
#### 样例解释
##### 样例 $1$
$v_1=0,v_2=1,v_3=0$。
##### 样例 $2$
$v_1=0,v_2=0,v_3=1,v_4=0$。
##### 样例 $3$
此样例与题图所对应。
#### 数据规模与约定
对于 $100\%$ 的数据,$1\le N\le 10^6$,$1\le X\le 10^{15}$。
#### 说明
**题目译自 [COCI2015-2016](https://hsin.hr/coci/archive/2015_2016/) [CONTEST #5](https://hsin.hr/coci/archive/2015_2016/contest5_tasks.pdf) *T4 POPLAVA***。