P6734 "Wdsr-2" Yin-Yang Orb.

Reimu Hakurei has a very, very large Yin-Yang Orb, which is one of her main weapons. However, the energy of the Yin-Yang Orb comes from the owner's spiritual power (reiryoku, 灵力) gathered together. Therefore, Reimu always needs to maintain it in daily life. Simply put, Reimu uses reiryoku to obtain the energy required by the Yin-Yang Orb.

Reiryoku has Yin and Yang types. At the beginning, Reimu has only two Yang reiryoku, and they form a circle. Each time, Reimu can perform one of the following two operations: - Insert one Yang reiryoku between two adjacent reiryoku. - Remove one Yang reiryoku. To keep it stable, at any time, the number of reiryoku on this circle **must not be less than two**. Because the Yin/Yang property of reiryoku is not stable, once the neighborhood of some reiryoku changes (one more neighboring reiryoku appears, or one neighboring reiryoku disappears), it will flip between Yin and Yang (Yang becomes Yin, or Yin becomes Yang). However, if only the type (Yin/Yang) of its neighboring reiryoku changes, then it will not change. Reimu will keep adjusting the reiryoku until it **finally** becomes $n$ in total (it may be more than $n$ during the process). Then, starting from some point, Reimu will **in order** take off each reiryoku clockwise or counterclockwise. This will form a chain. Reimu will use the energy on the chain to strengthen her Yin-Yang Orb. Doing this is easy. But Reimu is very curious: how many different **chains** can be formed in total? Because of her preference, she may have $m$ constraints. The $i$-th constraint $(p_i,c_i)$ specifies what type the $p_i$-th reiryoku on the chain should be. If $c_i=0$, it should be Yin; otherwise, it should be Yang. Since the result may be very large, Reimu only needs the answer modulo $998244353$. Two chains are different if and only if there exists a position where the types are different.

The first line contains a positive integer $n$ and a non-negative integer $m$. When $m=0$, there are no constraints. Otherwise, the next $m$ lines each contain two non-negative integers $p_i,c_i$, with the meaning as described above.

One line containing a non-negative integer, representing the total number of possible chains modulo $998244353$.

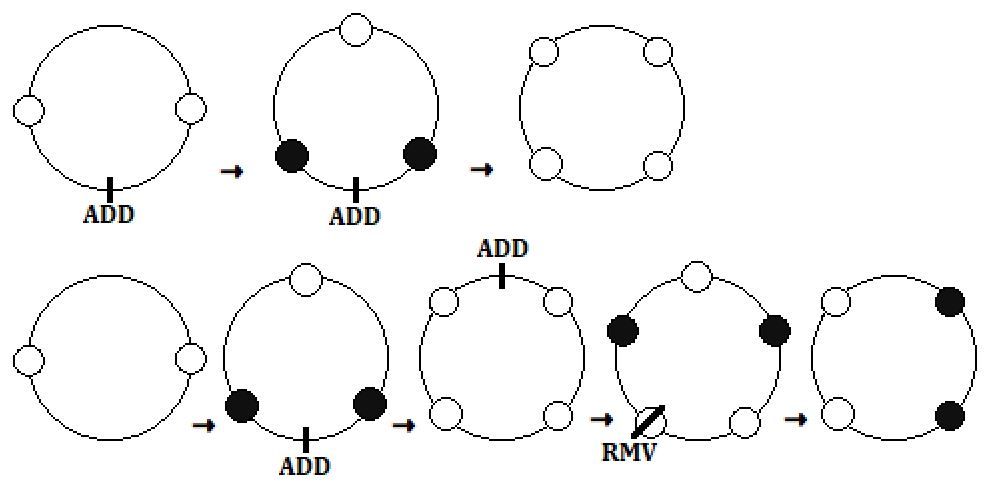
#### Sample Explanation For sample 1, the following two construction processes are possible:  Here, $\tt ADD$ means adding one Yang reiryoku, and $\tt RMV$ means removing one Yang reiryoku. After splitting the two resulting circles, we can obtain the following five different chains in total: - Circle 1: **Yang—Yang—Yang—Yang**. - Circle 2: **Yang—Yang—Yin—Yin**, **Yang—Yin—Yin—Yang**, **Yin—Yin—Yang—Yang**, **Yin—Yang—Yang—Yin**. Therefore, the answer is $5$. For sample 2, we restrict the first reiryoku on the chain to be Yang. Therefore, the result is $3$. #### Constraints $$\def\t{\text}\def\arraystretch{1.5} \begin{array}{|c|c|c|c|}\hline \textbf{Subtask} & n\t{ 的范围} & m\t{ 的范围} & \t{分值}\cr\hline 1 & n\le 16 & m\le 16 & 15 \cr \hline 2 & n\le 10^6 & m\le 5\times 10^3 & 40 \cr \hline 3 & n\le 10^{18} & m=0 & 15 \cr \hline 4 & n\le 10^{18} & m\le 5\times 10^3 & 30 \cr \hline \end{array}$$ In addition, for all testdata, $1\le p_i\le n,c_i\in \{0,1\}, 0\le m\le n$, and all $p_i$ are distinct. Translated by ChatGPT 5