P6738 [BalticOI 2014] Cop and Robber (Day1)

**This is an interactive problem.** ### Please use C++14/C++17 to submit to avoid unnecessary CE. ### You need to wrap your functions in `extern "C" { }`. Specifically, one way is as follows: ```cpp extern "C" { const int N = 500; int start(int n, bool a[N][N]) { // ... } int nextMove(int x) { // ... } } ```

A cop chases a robber. The cop will choose a street corner to guard. In each turn, the cop may choose to stay in place or move to an adjacent corner. The robber also starts at a street corner. Since he knows the map, he will choose the best strategy to move, but the robber is not allowed to stay in place. In each round, the cop moves first, then the robber moves. There are two possible outcomes: 1. The robber can avoid the cop forever. 2. At some street corner, the robber and the cop meet, and the robber is arrested. Determine whether the cop can catch the robber. If yes, output the minimum number of rounds. Your code must assume that the robber plays with a winning strategy. #### Interactive protocol You need to implement two functions to interact with the interactor. Their prototypes are: ```cpp int start(int N, bool A[MAX_N][MAX_N]); int nextMove(int R); ``` - `start(N, A)` passes in the following parameters: - $N$ — the number of street corners (corners are numbered from $0$ to $N - 1$). - $A$ — a 2D array describing the alleys: for all $0 \le i,\,j \le N-1$, if $i$ and $j$ are not connected, then $A[i,j]=\texttt{false}$, otherwise $A[i,j]=\texttt{true}$. All alleys are bidirectional (i.e. for all $i$ and $j$, $A[i,j]=A[j,i]$), and there are no self-loops (i.e. for all $i$, $A[i,i]=\texttt{false}$). In addition, you may assume that the cop can always reach any street corner from any other street corner through the alleys. If the cop can catch the robber on the map described by the parameters, the function `start` should return the index of the street corner where the cop and robber will meet. Otherwise, return $-1$. - `nextMove(R)` is given the parameter $R$, which is the index of the street corner where the robber is currently located. The function should return the index of the street corner where the cop is located after this move. The function `start` will definitely be called once before the first call to `nextMove`. If `start` returns $-1$, then `nextMove` will not be called. Otherwise, `nextMove` will be called repeatedly until the chase ends. More precisely, the program must terminate as long as one of the following happens: - `nextMove` returns an illegal move. - The robber can avoid the cop forever. - The robber is caught.

None

None

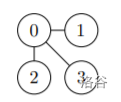
#### Sample explanation For sample $1$, the graph is as shown below:  The function call process is as follows: |Function call|Function return| |:-:|:-:| |`start(4, [[0, 1, 1, 1], [1, 0, 0, 0], [1, 0, 0, 0], [1, 0, 0, 0]])`|`3`| |`nextMove(1)`|`3`| |`nextMove(0)`|`0`| #### Constraints and notes **This problem uses bundled testdata.** - Subtask 1 (16 pts): No multiple edges. - Subtask 2 (14 pts): The map is grid-shaped, as follows:  - Subtask 3 (30 pts): $2 \le N \le 100$. - Subtask 4 (40 pts): $2 \le N$. For $100\%$ of the data, $1 \le N \le 500$. Thanks to the interactive library and SPJ author @[tiger2005](https://www.luogu.com.cn/user/60864). **This problem forces $O2$ optimization.** #### Notes Translated from [BalticOI 2014 Day1 A Cop and Robber](https://boi.cses.fi/files/boi2014_day1.pdf). Translated by ChatGPT 5