P6748 『MdOI R3』Fallen Lord

Ruling the world, ruling loneliness.

Country L has $n$ cities, and there are $n-1$ roads between them, forming a tree structure. King L sends some troops to guard these roads. The combat power of the troops guarding each road can be measured as an integer in $[1,m]$. Each city has a city lord. The $i$-th city lord has a tolerance value $a_i$. If the **median** of the combat powers of the troops stationed on all roads connected to the $i$-th city exceeds the **city lord**'s tolerance, then the **city lord** will think the king does not trust him and will want to rebel. Of course, King L does not want anyone to rebel, but he also wants to make the total combat power of the troops guarding the roads **as large as possible** to ensure national defense. Now he has found the strongest OIer in Country L — you — to help him solve this problem. If no matter how the troops are arranged there will be someone who wants to rebel, output `-1`. **Note: For any $k$ numbers, their median is the $\left\lfloor\dfrac{k}{2}\right\rfloor+1$-th number after sorting these numbers in nondecreasing order.**

The first line contains two positive integers, representing $n,m$. The second line contains $n$ integers. The $i$-th number represents $a_i$. The next $n-1$ lines each contain two numbers $u_i,v_i$, representing a road directly connecting city $u_i$ and city $v_i$. **The input is guaranteed to form a tree.**

One line with one integer, representing the maximum total combat power.

For more samples, please [get them here](https://www.luogu.com.cn/paste/0wcdzik5). For all testdata, $1\le u_i,v_i \le n\le 5\times 10^5$, $n\ge 2$, $1\le a_i\le m\le 10^9$. |Subtask ID|$n\leq$|$m\leq$|Other properties|Score| |:-:|:-:|:-:|:-:|:-:| |1|$8$|$8$|None|$5$| |2||$1$|None|$1$| |3|||The tree is a chain|$10$| |4|||There exists a node with degree $n-1$|$12$| |5|$10^5$||Each node has degree $\le 6$|$17$| |6|$5\times 10^3$||None|$20$| |7|||None|$35$| Blank entries mean they are the same as the $100\%$ Constraints. 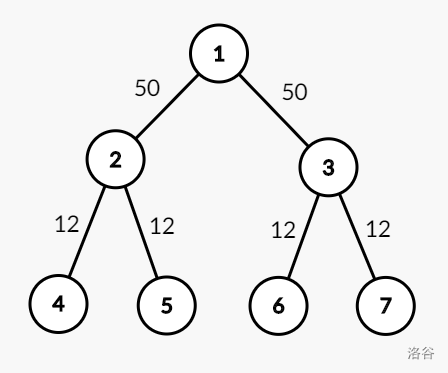### Sample Explanation  As shown in the figure, the combat powers of the troops guarding the $n-1=6$ roads (in the input order) are $50,50,12,12,12,12$, respectively. Translated by ChatGPT 5