P6804 [CEOI 2020] 权力药水

3s，256MB

很久以前，在萨满之岛上，所有人都住在一个如天一样高的豆茎上。每位萨满都有一个独一无二的编号，编号的范围在 $0$ 和 $N-1$ 之间。第 $i$ 位萨满居住的高度用 $H_i$ 表示。定义两位萨满间的距离为其高度差的绝对值。 所有的萨满之间本来和谐共处，直到一天权力药水的配方被盗。为了掩盖他的行径，那位小偷给整座岛施加了诅咒，大多数居民不再彼此信任了。 虽然情况非常复杂，但是经过调查，某组织还是获得了如下信息： - 诅咒刚生效时，所有的萨满停止彼此信任。 - 诅咒本身是不稳定的，在每天将要结束时（准确来说是午夜），某一对萨满将会建立信任或是停止信任。 - 不幸地是，一位萨满在任意时刻最多信任 $D$ 位萨满。 该组织还重建了萨满间的信任变化日志，该日志记录了在每个半夜，哪对萨满的信任关系发生了变化（从不信任到信任，或是从信任到不信任）。 该组织的成员相信，小偷还向一位邪恶的萨满通过隔空传话的方式泄露了配方。为了避免被发现，他们俩都各自拜访了一位信任的萨满的家，在拜访的过程中，小偷透过窗户向邪恶的萨满泄露配方。需要注意的是，那位信任的朋友当时不必在家中，事实上，两位萨满可能互相前往对方的家。毕竟萨满都很奇怪。 幸运的是，因为萨满们的听力有限，声音并不能传出太远，这意味着两位朋友（小偷的朋友和邪恶的萨满的朋友）之间的距离必须尽可能近。 现在该组织决定让你来协助调查。他们想要验证自己的猜想：当小偷为 $x$，邪恶的萨满为 $y$，泄露配方的日子为 $v$ 时，隔空传话的声音需要行进的最小值是多少？也即，你需要在第 $v$ 天时，在 $x$ 信任的所有萨满中找到一位萨满 $x'$，在 $y$ 信任的所有萨满中找到一位萨满 $y'$，使 $x'$ 和 $y'$ 间的距离最小。 你已经获得了求出答案所需的所有信息，但你需要**实时**回答每一组询问。

**仅提供 IO 交互**。 输入第一行包含四个整数 $N,D,U,Q$，分别代表萨满的数量，一位萨满最多信任的朋友数，日志包含的天数，以及需要回答的询问数。 下一行包含 $N$ 个整数，两两间以一个空格隔开。其中第 $i$ 个整数代表第 $i-1$ 只萨满居住的高度 $H_{i-1}$。 接下来 $U$ 行，第 $i$ 行包含两个整数 $A_i,B_i$，代表编号为 $A_i$ 和 $B_i$ 的萨满在第 $i-1$ 天结束的时候，他们之间的信任状态发生了变化。即，如果 $A_i$ 和 $B_i$ 在第 $i-1$ 天互相信任，则他们自第 $i$ 天起不再互相信任，反之同理。 接下来你需要回答 $Q$ 组询问。询问必须实时回答，即你必须回答完一组询问后才能读入下一组询问。 每组询问包含三个整数 $x,y,v$，代表小偷为 $x$，邪恶的萨满为 $y$，泄露配方的日子为第 $v$ 天。

对于每组询问，你需要在第 $v$ 天时，在 $x$ 信任的所有萨满中找到一位萨满 $x'$，在 $y$ 信任的所有萨满中找到一位萨满 $y'$，使 $x'$ 和 $y'$ 间的距离最小，并输出这个最小值。 特别地， - 若存在一位萨满同时被 $x$ 和 $y$ 信任，输出 $0$。 - 若 $x$ 或 $y$ 在第 $v$ 天无信任的朋友，输出 $1000000000$（$10^9$）。 在回答完一组询问后，你需要立刻刷新缓冲区。 对于 C++ 选手，可以通过 `fflush(stdout);` 或 `cout.flush()` 来刷新缓冲区。

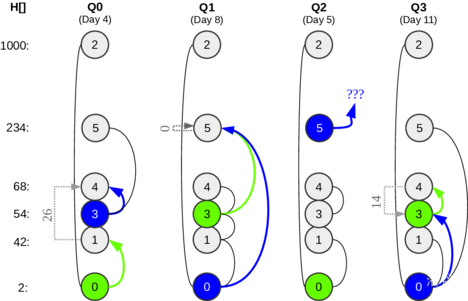
### 样例解释 下面是询问的情况：  下面是每一天时信任关系的变化情况：  ### 子任务 所有数据均满足：$2 \leq N \leq 10^5$，$1 \leq D \leq 500$，$0 \leq U \leq 2 \times 10^5$，$1 \leq Q \leq 5 \times 10^4$。 各子任务的约束条件如下： | 子任务编号 | 分值 | 约束 | | ---------- | ---- | --------------------------------------- | | $1$ | $0$ | 样例 | | $2$ | $17$ | $Q,U \leq 10^3$ | | $3$ | $14$ | 所有询问均满足 $v=U$ | | $4$ | $18$ | $\forall i \in [0,N)$，$H_i\in \{0,1\}$ | | $5$ | $21$ | $U,N \leq 10^4$ | | $6$ | $30$ | 无特殊约束 |