[Cnoi2020] 梦原

> 成熟是一种明亮而不刺眼的光辉，一种圆润而不腻耳的音响，一种不再需要对别人察言观色的从容，一种终于停止向周围申述求告的大气，一种不理会哄闹的微笑，一种洗刷了偏激的淡漠,一种无须声张的厚实，一种并不陡峭的高度。勃郁的豪情发过了酵，尖利的山风收住了劲，湍急的溪流汇成了湖。 ——余秋雨《文化苦旅》 在一个偶然的梦境中，Cirno 发现了一棵树，在一望无际的昏暗平原上，发出了淡淡的蓝色荧光。 Here lies $\ \ \ \ \ \ \ \ \ $.

不幸的是，这棵树尚未长成，只有一个根节点 $1$。 Cirno 只能知道这棵树将会有 $n$ 个结点，上面分别有 $a_1,a_2,\ldots,a_n$ 颗果实，却无法知道树的形状。 但是树的生长总是具有某种规律。 对于结点 $i$，它会**等概率地**从 $[i-k,i-1] \cap N^+$ 中选择一个结点连接，并成为那个节点的子节点。 其中，$k$ 是一个 Cirno 已经测出的常数。 为了摘下所有的果实，在树长成之后，Cirno 会多次使用魔法。其中每次会在树上选一个联通块，并从联通块内每个结点上摘取一个果子（必须保证该联通块内**每个结点都有果子**）。 显然，Cirno 会采取**最佳策略**使得使用魔法的次数最少。 现在，Cirno 已经知道了 $n$，$k$ 和每个结点将会长出的果子数 $a_i$，请你帮她计算出她最少使用的魔法次数的数学期望。为了简单起见，你只需要输出答案除以 $998244353$ 的余数。

第一行输入两个整数 $n$，$k$，含义如上所述。 第二行输入 $n$ 个整数，表示 $a_1,a_2,\cdots,a_n$。

输出一行一个整数，表示答案。

3 2
2 1 3

499122180

10 1
580461319 261515299 384092031 741339597 746815717 566875585 354719606 821499852 330315651 349091676

553073655

10 9
497873025 114058764 159468194 207476408 138162972 678927661 223886159 325207554 470061543 658861685

180853894

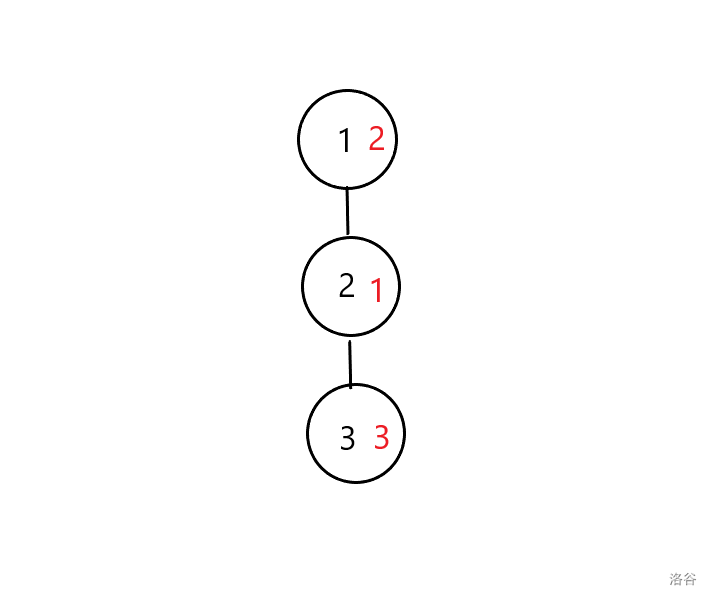
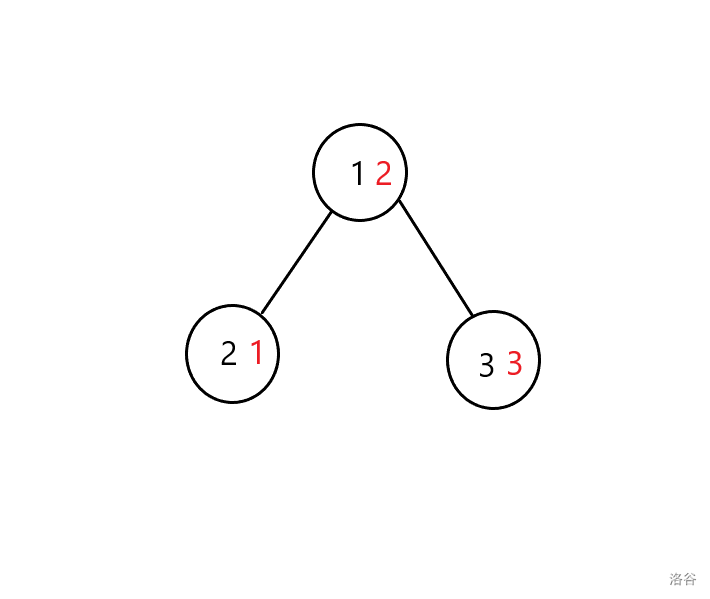
## 样例 1 解释： 可能长成的树有如下两种（黑色为结点编号，红色为结点上果子数）：  最佳方案是对联通块 $\{1,2,3\}$ 和 $\{1\}$ 各使用一次魔法，$\{3\}$ 使用两次，共四次。  最佳方案对联通块 $\{1,2,3\},\{1,3\}$ 和 $\{3\}$ 各使用一次魔法，共三次。 所以答案为 $\frac{7}{2}\equiv 499122180\pmod{998244353}$ ## 数据范围与约定 对于 $100\%$ 的数据，保证 $1\le k<n\le 10^6$，$0\le a_i<998244353$。 ### 子任务「本题采用捆绑测试」 - Subtask1（$10\%$）: $k=1$。 - Subtask2（$10\%$）: $n \le 10$，$a_i \in \{0,1\}$。 - Subtask3（$10\%$）: $n \le 10$。 - Subtask4（$10\%$）: $n \le 1000$。 - Subtask5（$60\%$）: 无特殊限制。