P6835 [Cnoi2020] Linear Creatures.

> In order to live happily in the Underworld rather than being sentenced to hell, humans have abandoned the practice of ending their own lives and are doing their best to live. From this perspective, humans seem somewhat positive and lovable. (Shameimaru Aya) Linear creatures move one-way toward the Underworld along a one-dimensional staircase. In that case, it only needs to climb step by step for $n$ steps to reach Hakugyokurou. But Cirno felt this was too monotonous, so the one-dimensional barrier was broken, and the chain-like road grew cauliflower-like branches.

A linear creature needs to walk from step $1$ to step $n+1$. At the beginning, for steps $1,2,3,\ldots,n$, each step has a directed edge to the next step $i\rightarrow i+1$. Then Cirno adds $m$ **atavistic edges** $u_i \rightarrow v_i (u_i \ge v_i)$, which form an **atavistic graph**. At each step, the linear creature will choose **uniformly at random** one outgoing edge from the current step and move to the corresponding step. When it reaches step $n+1$, it stops walking. Meanwhile, Cirno counts the total number of steps the linear creature takes, denoted by $\delta$. Cirno wants to know the value of $E(\delta)$ (i.e. the **mathematical expectation** of $\delta$) modulo $998244353$.

The first line contains three integers $id$, $n$, and $m$. The next $m$ lines each contain two integers $u_i$ and $v_i$. $id$ indicates the subtask ID. The meanings of the other letters are the same as above.

One line with one integer: $E(\delta)$. The meanings of the letters are the same as above.

## Required Mathematical Knowledge - **Power series summation that may be used**: If $x>1$, then $\sum\limits_{i=1}^{\infty}\big(\frac{1}{x}\big)^i=\frac{1}{x}+\frac{1}{x^2}+\frac{1}{x^3}+\cdots=\frac{1}{x-1}$. - **Mathematical expectation**: In a random experiment, the sum of the probability of each possible outcome multiplied by its outcome, reflecting the average value of a random variable. - **Discrete expectation formula**: $E(x)=\sum\limits_{k=1}^{\infty}x_kp_k$. ## Constraints and Conventions For $100\%$ of the testdata, it is guaranteed that $id \in \{1,2,3,4,5\}$, $0 < n,m \le 10^6$, and $1 \le v_i \le u_i \le n$. #### Subtasks (This problem uses bundled evaluation) - Subtask1 ($10\%$): In the atavistic graph, every node has a self-loop and all edges are self-loops (not drawn). The whole graph looks like:  - Subtask2 ($10\%$): In the atavistic graph, every node has an edge to and only to its predecessor. In particular, the predecessor of node $1$ is node $1$. The whole graph looks like:  - Subtask3 ($10\%$): In the atavistic graph, every node has an edge to and only to node $1$. 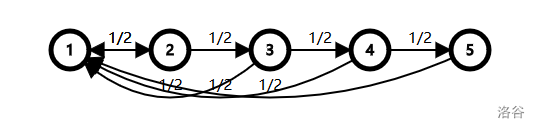The whole graph looks like:  - Subtask4 ($10\%$): $n \le 100$, $m \le 1000$. - Subtask5 ($60\%$): No special restrictions. ## Postscript The problem name comes from Touhou Kikeijuu (th17), Stage 6 Boss Keiki Haniyasushin, Hard / Lunatic difficulty spell card: 線形「リニアクリーチャー」. Translated by ChatGPT 5