P6840 [BalkanOI 2009] year2012 - A New Beginning

[English statement](/problem/U126972) | [Source](http://www.cs.org.mk/boi2009/tasks.html) The maximum running time of the official solution on the largest test is 1.56 s, so the time limit for this problem is 2 s.

An extreme solar flare heated up the Earth and caused a huge disaster. Crust plates are freely floating in the mantle; earthquakes of unknown magnitude are making megacities collapse; mountains are being flooded by gigantic tsunamis; countries are turning into oceans of lava and volcanic ash. It is now December 21, 2012, and your only chance to save yourself and your family from the end of the world is to board the government ship on the Himalayas, a modern ark to save humanity. You have an airplane that flies at a constant speed and a map with all fixed airports. Unfortunately, not all airports are connected—huge volcanic ash clouds block some routes, and other airports are too far apart. Also, not all airports have fuel supply—some airports have nothing left but bare runways—and you cannot refuel there. Since all navigation methods have been destroyed, the only possible path between two airports is the shortest one. Most importantly, due to atmospheric instability and sharp changes in air density, the engine’s fuel efficiency may differ during flight. Therefore, the fuel consumption also differs. The good news is that you know which pairs of airports you can fly between, how much fuel each flight needs, and where you can refuel. All you need to do is find a way to reach the Himalayas airport as fast as possible. Write a program `year2012` that, given the coordinates of each airport, whether it has fuel, the plane’s fuel tank capacity, the plane’s speed, several pairs of airports that have a possible connection, and the fuel needed for each flight, computes the minimum time needed to complete the mission.

Read from standard input. The first line contains four integers (translator’s note: the sample does not strictly follow this rule; for the exact constraints, it is recommended to refer to the “Hint” section) $N, M, V, C$, representing the number of airports, the number of available routes, the constant speed of the airplane, and the fuel tank capacity. The next $N$ lines each contain three real numbers $X_i, Y_i, Z_i$ and a boolean value $R_i$. The three real numbers are the 3D coordinates of airport $i$. $R_i = 0$ means you cannot refuel at this airport, and $R_i = 1$ means you can refuel. The next $M$ lines each contain three integers $A_k, B_k, F_k$, describing a route between two airports and the fuel needed. Each route is bidirectional. The last line contains two integers $S, T$, representing the first and the last airport of the trip.

Write to standard output. Output one line with one real number, the minimum time from $S$ to $T$. If the absolute error of your answer compared with the standard answer is at most $10^{-4}$, it will be considered correct. If you cannot reach the destination, output $0$.

**Constraints** - Number of airports $N \in \left[2, 10^3\right] \cap \Z$. - Number of available routes $M \in \left[1, 10^4\right] \cap \Z$. - Constant plane speed $V \in \left[1, 10^3\right]$ is a real number with at most $3$ digits after the decimal point. - Fuel tank capacity $C \in \left[1, 10^3\right] \cap \Z$. - Airport coordinates $X_i, Y_i, Z_i \in \left[-100, 100\right]$ are real numbers with at most $18$ digits after the decimal point. Also, it is guaranteed that $X_i^2 + Y_i^2 + Z_i^2$ is the same for all $i$. In other words, for one testdata, all airports have the same distance to the Earth’s center. - Number of airports where you can refuel $\in \left[1, 20\right] \cap \Z$. - The Earth radius is an integer not less than $1$. - Route endpoints $A_k, B_k \in \left[1, N\right] \cap \Z$ and $A_k \ne B_k$. Each route appears at most once. - Fuel cost of a route $F_k \in \left[1, C\right] \cap \Z$. **Notes** - The distance of a route is the shortest arc on the sphere. There may be multiple such arcs, but we only care about the distance. - All route distances are at least $10^{-6}$. - Due to possible precision errors in floating-point computations, the distance from an airport to the Earth’s center may differ slightly. However, the testdata guarantees that the absolute error of all distances is at most $10^{-10}$, so the correctness of the algorithm is not affected. - $R_s = 1$, which means the plane’s tank is full at the beginning. Each time you pass through an airport where you can refuel, the tank will be filled up again. - Landing, refueling, takeoff, and acceleration can be ignored, i.e. treated as $0$. - All available routes are independent from each other. This means that if there is a route from $A$ to $B$ passing by $C$, it does not imply that there is an available route from $A$ to $C$, or from $B$ to $C$. **Subtasks** For $40\%$ of the data, $N \le 8$. 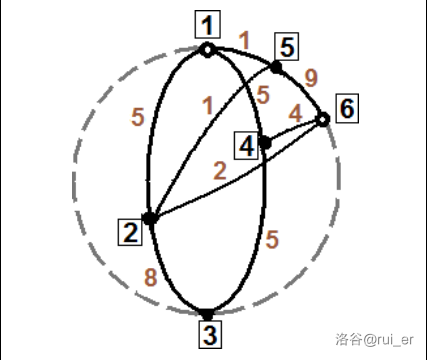--- **Sample Explanation**  The Earth radius is $5$. The plane speed is $2.5$, and the fuel tank capacity is $9$. We want to go from $1$ to $3$. In the figure, black solid lines are available routes, airport indices are inside rectangles, and fuel costs are labeled next to the black lines. Airports where you can refuel are hollow points. Clearly, we cannot directly use $1 \rightarrow 2 \rightarrow 3$ or $1 \rightarrow 4 \rightarrow 3$—their fuel costs are $13$ and $10$, which exceed the tank capacity. In fact, all routes cost more than $9$ fuel, so we must pass through airport $6$. We have three possible routes: $1 \rightarrow 2 \rightarrow 6$, $1 \rightarrow 4 \rightarrow 6$, and $1 \rightarrow 5 \rightarrow 2 \rightarrow 6$. The first two are obviously the shortest (routes $1 \rightarrow 2$, $5 \rightarrow 2$, $2 \rightarrow 6$, $1 \rightarrow 4$, and $4 \rightarrow 6$ take the same amount of time). After we refuel to full at airport $6$, if we go to airport $2$, we still cannot reach the destination—we are short of one unit of fuel. One feasible route is to go through $4$, and then use up all fuel to reach $3$. Finally, the routes we can choose are $1 \rightarrow 2 \rightarrow 6 \rightarrow 4 \rightarrow 3$ and $1 \rightarrow 4 \rightarrow 6 \rightarrow 4 \rightarrow 3$. Both have four right-angle turns, so their total lengths are equal, both equal to the circumference of the Earth’s equator, i.e. $2 \pi R$. Therefore, the time cost is $\dfrac{2 \pi R}{V} \approx 12.566370614359172953850573533118$. Translated by ChatGPT 5