P6840 [BalkanOI 2009] year2012 - A New Beginning

[英文题面](/problem/U126972) | [题目来源](http://www.cs.org.mk/boi2009/tasks.html) 本题官方题解最大点时间 1.56s，故本题时间限制 2s。

一次极端的太阳爆发使地球升温，造成了一场巨大的灾难。地壳板块在地幔中自由浮动；震级未知的地震正在导致大都市倒塌；山峦被巨大的海啸淹没；各国正转向熔岩和火山灰的海洋。 现在是 $2012$ 年 $12$ 月 $21$ 日，你唯一能让你和你的家人免于世界末日的机会就是登上喜马拉雅山的政府船，这是拯救人类的现代方舟。你有一架匀速飞行的飞机和一张有所有固定机场的地图。不幸的是，并不是所有的机场都连接在一起——巨大的火山灰云阻塞了一些航线，而其他机场却相距太远。此外，并不是所有的机场都有燃料供应——有些机场除了光秃秃的道路什么都没有留下——而且在那里你无法给飞机加油。由于所有的导航手段都被摧毁了，两个机场之间唯一可能的路径就是最短的一条。最重要的是，由于大气不稳定和空气密度的急剧变化，发动机的燃油效率在飞行中会有所不同。因此油耗也不同。好的新情况是你知道在哪一个机场可以飞行，所需的燃料量，以及你可以在哪里加油。你所要做的就是想办法尽快从机场到喜马拉雅山的机场。编写一个 `year2012` 程序，根据每个机场的坐标、是否有燃油、飞机的油箱容量、飞机的速度、一个潜在的航班连接的几对机场以及每一次飞行需要多少燃料，计算完成这项任务所需的最短时间。

从标准输入读入。 第一行四个整数（译者注：可以看到样例并没有严格遵守此规则，具体的数据范围建议以【提示说明】中的为准，下同）$N,M,V,C$，分别表示机场数量、可用航线数量、飞机恒定速度和油箱容量。 接下来 $N$ 行，每行由三个实数 $X_i,Y_i,Z_i$ 和一个布尔值 $R_i$ 组成。三个实数表示 $i$ 号机场的空间坐标， $R_i=0$ 表示不能在这个机场加油，$R_i=1$ 表示可以加油。 接下来 $M$ 行，每行三个整数 $A_k,B_k,F_k$，表示这条航线的两端和花费的燃油量。每条航线都是双向的。 最后一行两个整数 $S,T$，表示路线上第一个和最后一个机场。

输出到标准输出。 一行，一个实数，表示从 $S$ 到 $T$ 的最短时间。如果你的答案与标准答案的绝对误差不超过 $10^{-4}$，你的答案将被认为是正确的。 如果你无法到达目的地，输出 $0$。

**数据范围** - 机场数量 $N\in\left[2,10^3\right]\cap\Z$。 - 可用航线数量 $M\in\left[1,10^4\right]\cap\Z$。 - 飞机恒定速度 $V\in\left[1,10^3\right]$ 为小数点后最多 $3$ 位的实数。 - 油箱容量 $C\in\left[1,10^3\right]\cap\Z$。 - 机场空间坐标 $X_i, Y_i, Z_i\in\left[-100,100\right]$，为小数点后最多 $18$ 位的实数。另外，保证 $X_i^2+Y_i^2+Z_i^2$ 对于所有 $i$ 均相同。换句话说，对于一个测试数据，所有的机场距离地心的距离均相同。 - 可以加油的机场数量 $\in\left[1,20\right]\cap\Z$。 - 地球半径为不小于 $1$ 的整数。 - 航线的两端 $A_k, B_k\in\left[1,N\right]\cap\Z$ 且 $A_k\ne B_k$。满足同一条航线只会出现一次。 - 航线花费的油量 $F_k\in\left[1,C\right]\cap\Z$。 **备注** - 一条航线的距离为球体上最短的弧。这种弧可能有很多个，但是我们只关心距离。 - 所有航线距离均不小于 $10^{-6}$。 - 由于实数运算可能的精度误差，每个机场到地心的距离可能略有不同。但是数据保证所有距离的绝对误差不超过 $10^{-10}$，因此算法的正确性不受影响。 - $R_s = 1$，这意味着飞机的油箱初始是满的。每次路过一个可以加油的机场，油箱将会再次加满。 - 飞机降落、加油、起飞、加速的过程可以被忽略，即认为是 $0$。 - 所有可用的航线都是彼此独立的。这意味着如果有航线从 $A$ 到 $B$，路过 $C$，这不代表有从 $A$ 到 $C$、或从 $B$ 到 $C$ 的可用航线。 **部分分** 对于 $40\%$ 的数据，$N\le 8$. 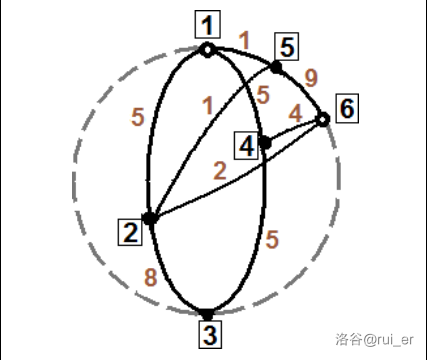--- **样例解释**  地球的半径为 $5$。飞机速度为 $2.5$，油箱容量为 $9$。我们想要从 $1$ 到 $3$。如图，黑实线代表可用的航线，机场编号在矩形的内部，油量花费在黑实线边上备注。我们可以加油的机场的点是空心的。显然，我们不能直接通过 $1\rightarrow 2\rightarrow 3$ 或者 $1\rightarrow 4\rightarrow 3$——它们的油量花费分别为 $13$ 和 $10$，超过了油箱的最大容量。事实上，所有路线都花费了大于 $9$ 的燃油，因此我们必须经过 $6$ 号机场。我们有三条可能的路线：$1\rightarrow 2\rightarrow 6$、$1\rightarrow 4\rightarrow 6$ 和 $1\rightarrow 5\rightarrow 2\rightarrow 6$。前两种显然是最短的两个（航线 $1\rightarrow 2$、$5\rightarrow 2$、$2\rightarrow 6$、$1\rightarrow 4$ 和 $4\rightarrow 6$ 花费同样长的时间）。在我们在 $6$ 号机场加满油后，如果我们前往 $2$ 号机场，我们依然不能到达目的地——我们缺少一个单位的燃油。为一可行的路线是通过 $4$，然后花光所有燃油到达 $3$。最后，我们可选的路线有 $1\rightarrow 2\rightarrow 6\rightarrow 4\rightarrow 3$ 和 $1\rightarrow 4\rightarrow 6\rightarrow 4\rightarrow 3$。他们都有四个直角弯，因此它们的总长度相等，都等于地球的赤道周长，或 $2\pi R$。因此，花费的时间为 $\dfrac{2\pi R}{V}\approx 12.566370614359172953850573533118$。