P6842 [BalkanOI 2009] Strip

[English statement](/problem/U126974) | [Source](http://www.cs.org.mk/boi2009/tasks.html)

Let us consider a strip with width $1$, length $n$, and negligible thickness, made of unit squares. As shown in the figure (where $n=7$), starting from the left side of the strip, we label each vertical line with the non-negative integers from $0$ to $n$. We are only allowed to fold the rectangular strip along these vertical lines, and after that the two parts are glued together and will never be straightened again.  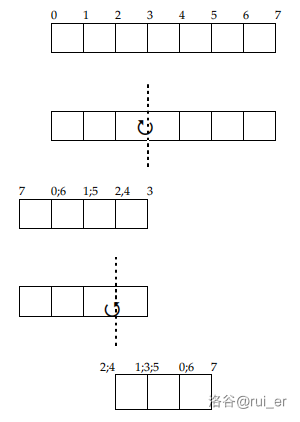Naturally, after folding, some labels will overlap and form a vertical line with more labels. The figure shows the situation after folding along vertical line $3$. After this operation, some lines will have two labels. For example, we can say either $1$ or $5$; they refer to the same vertical line. If we then fold along $2$ (we can also say $4$, it is the same), there will be a vertical line with even three names, as we can see: $(1;3;5)$. For example, if we fold the rectangular strip along line $3$, we only rotate the strip without changing its labels or length. We call such a fold “empty”: it is **not** illegal, it just does not make any significant change. In this way, a sequence of $k$ integers (each integer from $0$ to $n$) uniquely defines how the strip is folded. Write a program to find the length of the strip after all folds are completed.

Read from standard input. - The first line contains two positive integers $n,k$, representing the length of the strip and the number of folds. - The second line contains $k$ non-negative integers, representing the folding order, and each number is in the range $\left[0,n\right]$.

Write to standard output. One line with one integer, representing the length after folding.

**Constraints** $n$ has at most $18$ digits, and $k\le 10000$. --- **Explanation of Sample $2$** The folding steps are shown in the figure: Initial state: $\{0\,1\,2\,3\,4\,5\,6\,7\,8\,9\}$. Folding steps: $\rightarrow \{0\,(1;9)\,(2;8)\,(3;7)\,(4;6)\,5\}\rightarrow \{(1;9)\,(0;2;8)\,(3;7)\,(4;6)\,5\}\rightarrow \{(0;2;8)\,(1;3;7;9)\,(4;6)\,5\}\rightarrow \{(1;3;7;9)\,(0;2;4;6;8)\,5\}$. (Note: Sample $1$ is the same as the picture.). Translated by ChatGPT 5