P6845 [CEOI 2019] Dynamic Diameter
题目描述
有一棵树,含 $n$ 个节点,边带权。
会有 $q$ 次修改,每次会将树上的一条边的边权进行修改,在每次修改后,您需要求出每次修改后,这棵树的直径上的边权和。
**本题强制在线。**
输入格式
第一行为三个整数 $n,q,w$,分别表示点的个数,询问的个数和边权的上限。
接下来 $n-1$ 行,每一行为三个整数 $a_i,b_i,c_i$,表示 $a_i$ 到 $b_i$ 有一条边权为 $c_i$ 的边。
接下来 $q$ 行,每行两个经过加密的整数 $d_j,e_j$。
解密方式如下:
- $d_j'=(d_j+\text{last})\bmod(n-1)$
- $e_j'=(e_j+\text{last})\bmod w$
其中 $\text{last}$ 表示上一个询问的答案,初值为 $0$。
表示将第 $d_j'+1$ 条边的边权改为 $e_j'$。
输出格式
共输出 $q$ 行,一行一个整数,第 $i$ 行的整数表示在第 $i$ 次修改后的直径上的权值总和。
说明/提示
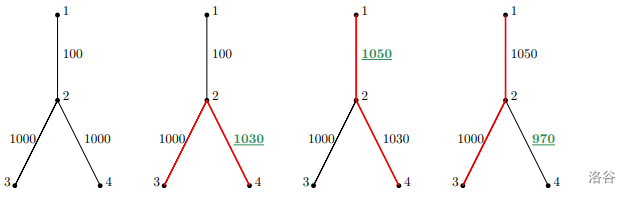
#### 样例 1 解释
解密后的修改如下:
```
2 1030
0 1050
2 970
```
如图为树的边权变化过程,红边代表树的直径:
#### 数据范围
对于 $100\%$ 的数据,保证 $2\le n\le 10^5$,$1\le q\le 10^5$,$1\le w\le 2\times 10^{13}$,$1\le a_i,b_i\le n$,$0\le c_i,e_j