P6848 [CEOI 2019] Scissors and Tape

您有一个简单多边形 $S$，现在您想将其变成与其面积相等的简单多边形 $T$。 您可以使用两种工具：剪刀和胶带。剪刀可将任何多边形切割成较小的多边形。胶带可将较小的多边形组合成较大的多边形。您可以按任何顺序多次使用每个工具。 输入中的多边形的顶点坐标均为整数，但您的方案允许产生顶点坐标不为整数的多边形。 任务的形式化定义如下： 一个形状 $Q=(Q_0,\ldots Q_{n-1})$ 是平面中三个点及以上的序列，满足： - 闭合折线 $Q_0,Q_1,Q_2,\ldots Q_{n-1},Q_0$ 不相交。 - 这段折线以逆时针围绕多边形的边界。 以形状 $Q$ 为边界的多边形为 $P(Q)$。 两个形状等效当且仅当一个形状经过平移或旋转之后与另一个形状相同。 不允许对形状进行对称，且点的顺序与形状有关：$(Q_0,Q_1\ldots Q_{n-1})$ 不一定等价于 $(Q_1\ldots Q_{n-1},Q_0)$。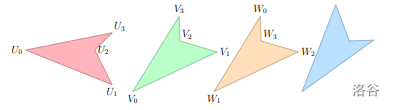  在上图中，形状 $U$ 和 $V$ 是等价的，但形状 $W$ 与他们不等价，原因是给出的点的顺序不同，无论如何，第四个形状都不与前三个形状相同，因为不允许对称形状。 每一个形状的表示由 $2\times n+1$ 个数组成，第一个数为 $n$，表示形状的点数，接下来 $2\times n$ 个数 $Q_{0,x},Q_{0,y},Q_{1,x},\ldots,Q_{n-1,x},Q_{n-1,y}$，每两个数均表示形状里一个点的坐标，如 $(Q_{0,x},Q_{0,y})$ 为 $Q_0$ 的坐标。 形状 $B_1,B_2,\ldots B_k$ 被称为形状 $A$ 的划分，当且仅当： - 所有 $P(B_i)$ 的并集为 $P(A)$。 - 对于所有的 $i\not=j$，$P(B_i)$ 与 $P(B_j)$ 无交。 形状是有 ID 的，$S$ 的 ID 为 $0$，您在解决方案中生成的 ID 为 $1,2,3,\ldots$。 剪刀将会剪开一个现有的形状 $A$，并产生 $A$ 的一个划分 $B_1,B_2,\ldots B_k$。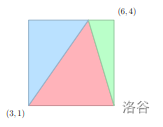  在上图中，形状 $A$ 被划分成了 $B_1,B_2,B_3$ 三个三角形。其中描述红色三角形的一种方式为 `3 3 1 6 1 5.1 4`。 胶带可以粘合存在的形状 $A_1,\ldots A_k$ 并使其变成形状 $B$，要执行这个操作，需要给定 $C_1,\ldots,C_k$ 和最终形状 $B$ 并满足如下要求： - $C_i$ 等价于 $A_i$。 - $C_1,\ldots,C_k$ 是 $B$ 的划分。 通俗地说，你选择了形状 $B$，然后展示如何把每个存在的 $A_i$ 移动到构成 $B$ 的正确的位置 $C_I$。注意形状 $B$ 需要分配一个新 ID，但 $C_i$ 不需要。

第一行为形状 $S$。 第二行为形状 $T$。

每当使用剪刀时，按如下格式输出： ``` scissors id(A) k B_1 B_2 ... B_k ``` 每当使用胶布时，按如下格式输出： ``` tape k id(A_1) ... id(A_k) C_1 C_2 ... C_k B ``` 您的输出需要保证以下限制： - 输出的所有点坐标在 $[-10^7,10^7]$ 之内。 - 输出的每个形状最多能有 $100$ 个点。 - 每次操作中，$1\le k\le 100$。 - 操作数不多于 $2\times 10^3$。 - 输出中所有形状的总点数不超过 $2\times 10^4$。 - 最后必须只剩下一个形状，且这个形状等价于 $T$。

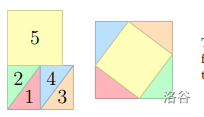
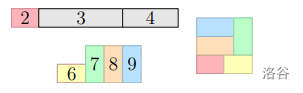
#### 样例解释 #### 样例 1 解释  上左图是使用剪刀操作后的原始图形，右侧是使用胶带后对应 $C_i$。 #### 样例 2 解释 请注意，目标和您的最后达成的多边形只需等价即可，不需完全相同。 #### 样例 3 解释 下图显示了这个样例输出的三个阶段：  #### 数据范围及限制 对于 $100\%$ 的数据，保证 $S$ 与 $T$ 的点数 $\le 10$ 且 $\ge 3$，输入的所有点坐标在 $[-10^6,10^6]$ 之内，无三点共线的情况，$P(S)$ 与 $P(T)$ 的面积相等。 如果一个形状的顶点分别为 $(0,0),(x,0),(0,y),(x,y)$ 且 $x,y$ 为正整数，则称它为好矩形。 如果一个形状是好矩形且 $x=y$，则称它为好正方形。 如果多边形 $P(A)$ 的每个内角都小于 $180$ 度，则称形状 $A$ 为严格凸多边形。 详细子任务限制如下： | 子任务编号 | 限制 | 分数 | | :-: | :-: | :-: | | 1 | $S$ 和 $T$ 是好矩形且输入的所有点坐标在 $[1,10]$ 之内 | $5$ | | 2 | $S$ 是好矩形且 $x>y$，$T$ 是好正方形 | $13$ | | 3 | $S,T$ 是好矩形 | $12$ | | 4 | $S$ 是三角形，$T$ 是好正方形 | $14$ | | 5 | $S,T$ 均是三角形 | $10$ | | 6 | $S$ 是严格凸多边形，$T$ 是好矩形 | $16$ | | 7 | $T$ 是好矩形 | $11$ | | 8 | 无特殊限制 | $19$ | #### 说明 本题译自 [Central-European Olympiad in Informatics 2019](https://ceoi.sk/) [Day 2](https://ceoi.sk/tasks/) [T3 Scissors and Tape](https://ceoi.sk/static/statements/scissors-ENG.pdf)。