P6874 [COCI 2013/2014 #6] KOCKICE

Stacking blocks.

Mirko and Slavko are playing with blocks. Each of them has their own pile of bricks. There are a total of $N$ columns of bricks (where $N$ is odd). In Mirko’s pile, the $i$-th column has $m_i$ bricks, and in Slavko’s pile, the $i$-th column has $s_i$ bricks. They decide to make the two piles identical. The heights must first strictly decrease and then strictly increase (see the right figure below). The heights of adjacent columns must differ by exactly $1$ (see the figure). The number of bricks on the left and right sides of the lowest column must be the same.  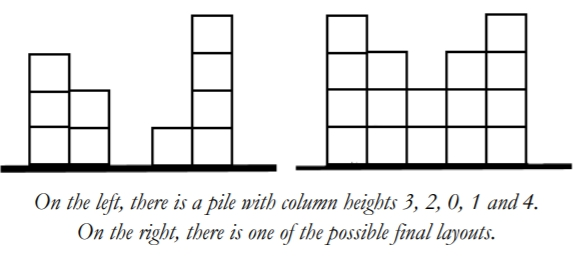Two operations are allowed: - Remove one brick from the top of a column. - Add one brick to the top of a column. Under the requirements above, find the minimum number of operations.

The first line contains an odd integer $N$, the number of columns in each person’s pile. The second line contains $N$ integers $m_i$, the column heights in Mirko’s pile. The third line contains $N$ integers $s_i$, the column heights in Slavko’s pile.

Output the minimum number of operations needed.

#### Explanation for Sample 1 Mirko puts two bricks on top of the first column of his pile, and Slavko puts one brick on top of the third column of his pile. #### Constraints - For $40\%$ of the testdata, $1\le N\le 1000$, $0\le m_i,s_i\le 1000$. - For $100\%$ of the testdata, $1\le N\le 3\times 10^5$, $0\le m_i,s_i\le 10^{12}$. #### Notes **This problem is translated from [COCI2013-2014](https://hsin.hr/coci/archive/2013_2014/) [CONTEST #6](https://hsin.hr/coci/archive/2013_2014/contest6_tasks.pdf) _T3 KOCKICE_.** Translated by ChatGPT 5