P6889 [CEOI 2006] CONNECT

Back in the day when the famous sixteen-bit three-letter operating system most often used on an 25x80 terminal dominated the PC market, "Nibbles" was everyone's favorite computer game. This problem, however, is not related to Nibbles – it is related to a game called "Connect" which is almost, but not quite, entirely unlike Nibbles. Connect is played on a board composed of squares organized into R rows and $C$ columns, where both $R$ and $C$ are **odd numbers**. Rows and columns are numbered $1$ to $R$ and $1$ to $C$, respectively. Each position on the board is either free or blocked by a wall. Additionally, each board satisfies the following constraints: - Squares with **both coordinates even** are called rooms. They are **never blocked**. - Squares with **both coordinates odd** are called barriers. They are **always blocked** - All other squares are called corridors. They may or may not be blocked. - Corridors **along the edge** of the board are **always blocked**. Barriers are represented by the '+' (plus) character, blocked horizontal corridors by the '|' (pipe) character, while blocked vertical corridors are represented by the '–' (minus) character. Rooms and free corridors are represented by the blank character. At the beginning of the game an **even number** of figures (represented by the uppercase letter 'X') are placed on the board – each in a separate **room**. $A$ path between figures $A$ and $B$ is a sequence of **free** squares starting from $A$, ending with $B$ and moving in one of the **four possible directions** in each step (the path includes both endpoint squares, $A$ and $B$). The length of the path is the total number of steps needed to get from $A$ to $B$ (which is equal to the number of squares contained in the path minus one). The goal of the player is to first **divide all the figures into pairs**, and then, for each pair, **connect** the two figures with a path. The pairs should be connected in such a way that **no two paths share a common square**. For a completed game, the score is defined as **the sum of the lengths** of all paths.  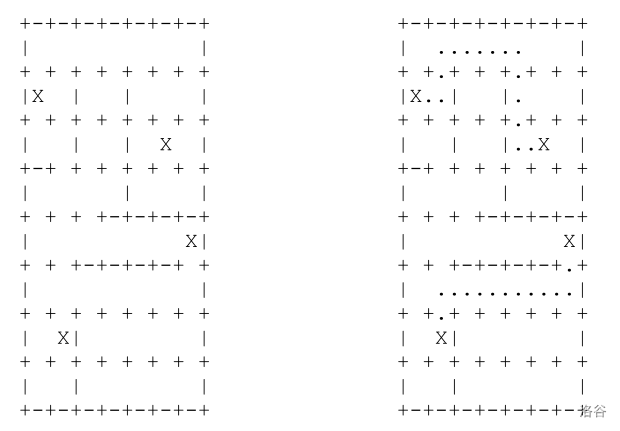Write a program that, given the starting position of the Connect game, plays the game in such a way that the **minimum possible score** is achieved. The test data will guarantee that a solution, although not necessarily unique, will always exist.

The first line of input is two integers: $R$ and $C$, where $R$ is the number of rows and $C$ is the number of columns. $R$ and $C$ are both odd numbers. The next $R$ lines each contain $C$ characters, each of which is one of `+`, `|`, `-`, space or `X`, representing obstacles and two types of walls, respectively, a space represents a room or a passable corridor, and `X` represents an item in the room.

The first line of output is an integer, which is the minimum score. This task **does not** require outputting a legal solution

$5 \leqslant R \leqslant 25$，$5 \leqslant C \leqslant 80$