P6931 [ICPC 2017 WF] Mission Improbable

这是一个春天的晴天，你即将见到 Patrick，他是你的密友和前犯罪伙伴。Patrick 因为在编程比赛中赌博而损失了大部分的钱，所以他需要再干一票。为此，他需要你的帮助，尽管你已经从犯罪生活中退休。你起初很不情愿，因为你不想回到过去的犯罪生活，但你觉得听听他的计划也无妨。 附近的一个仓库里有一批昂贵的消费品，Patrick 打算尽可能多地偷走这些物品。这需要找到进入建筑物的方法，制服保安，通过各种激光束——你知道的，通常的抢劫技巧。然而，仓库的核心部分配备了一个 Patrick 无法禁用的安全系统。这就是他需要你帮助的地方。 货物存放在大型立方体箱子中，所有箱子的尺寸相同。箱子整齐地堆叠在一起，形成一个三维网格。安全系统每小时使用三个摄像头拍摄这些堆叠：一个前置摄像头，一个侧面摄像头和一个顶部摄像头。前置摄像头的图像显示每列中最高堆叠的高度，侧面摄像头的图像显示每行中最高堆叠的高度，顶部摄像头的图像显示每个堆叠是否为空。如果安全系统检测到任何图像的变化，它就会发出警报。 一旦 Patrick 进入，他将确定堆叠的高度并发送给你。图 C.1 显示了网格的可能布局和每个摄像头的视图。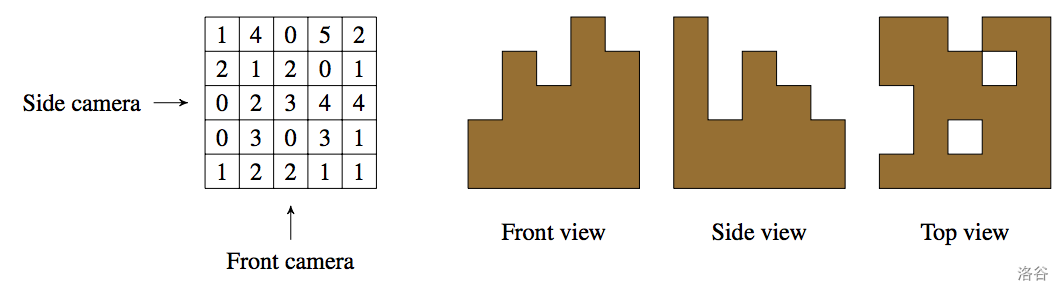  图 C.1：高度网格和相应的摄像头视图。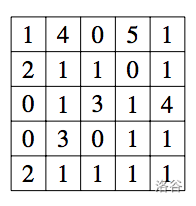  图 C.2：抢劫后的可能高度网格 Patrick 想要尽可能多地偷走箱子。由于他无法禁用安全系统，他计划通过将剩余的箱子重新排列成堆叠，使得下一组摄像头图像保持不变。在上述示例中，可以偷走九个箱子。图 C.2 显示了一个可能的抢劫后配置，看起来与安全系统相同。 Patrick 请求你帮助他确定在不被检测到的情况下可以偷走的最大箱子数量。你会帮助他完成这最后一票吗？

输入的第一行包含两个整数 $r (1 \le r \le 100)$ 和 $c (1 \le c \le 100)$，分别表示网格的行数和列数。接下来的 $r$ 行中的每一行包含 $c$ 个整数，表示对应行中堆叠的高度（以箱子为单位）。所有高度都在 $0$ 到 $10^{9}$ 之间（含）。

输出可以在不被检测到的情况下偷走的最大箱子数量。

时间限制：1 秒，内存限制：512 MB。 题面翻译由 ChatGPT-4o 提供。