P6947 [ICPC 2018 WF] Panda Preserve

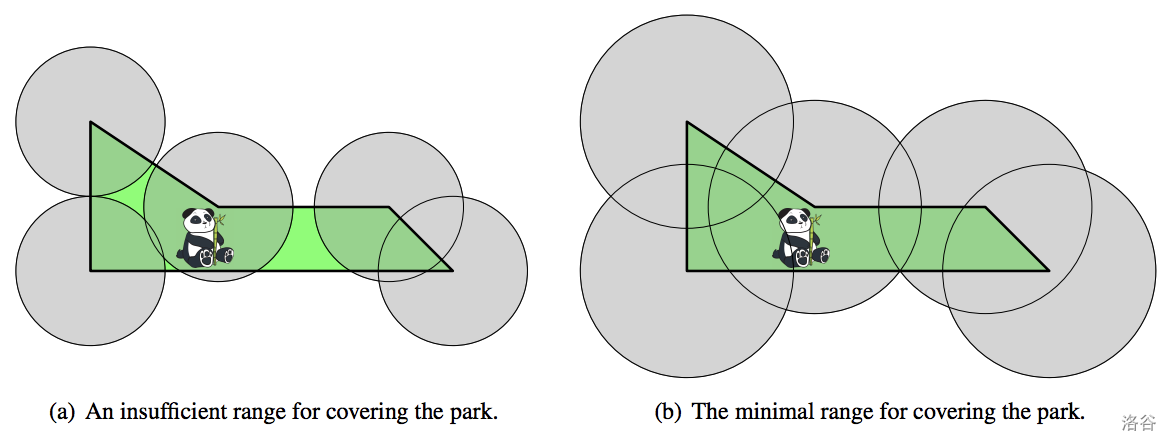
上个月，四川省获得资金建立大熊猫国家公园，这是一处为超过 1800 只大熊猫提供栖息地的自然保护区。公园将被多边形围栏包围。为了让研究人员追踪大熊猫，将在围栏的每个顶点放置无线接收器，每只大熊猫都将配备无线发射器。每个无线接收器将覆盖以接收器位置为中心的圆形区域，并且所有接收器的覆盖范围相同。显然，覆盖范围较小的接收器更便宜，因此你的目标是确定能够覆盖整个公园的最小可能范围。 例如，图 G.1 显示了由第一个样例输入描述的公园。注意，35 的无线范围不足以覆盖整个公园（a），而 50 的最佳范围则可以覆盖整个公园（b）。  图 G.1：样例输入 1 的示意图。

输入的第一行包含一个整数 $n (3 \le n \le 2000)$，表示公园边界多边形的顶点数。接下来是 $n$ 行，每行包含两个整数 $x$ 和 $y (|x|, |y| \le 10^{4})$，表示多边形顶点的坐标 $(x, y)$，按逆时针顺序给出。该多边形是简单多边形，即其顶点是不同的，且多边形的任意两条边不相交或接触，除非是相邻边在其公共顶点处接触。

输出能够覆盖整个公园的最小无线范围，绝对误差或相对误差不超过 $10^{-6}$。

时间限制：10 秒，内存限制：1024 MB。 题面翻译由 ChatGPT-4o 提供。