P6978 [NEERC 2015] Froggy Ford

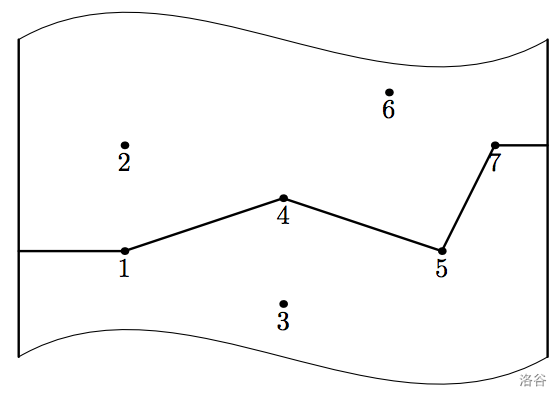
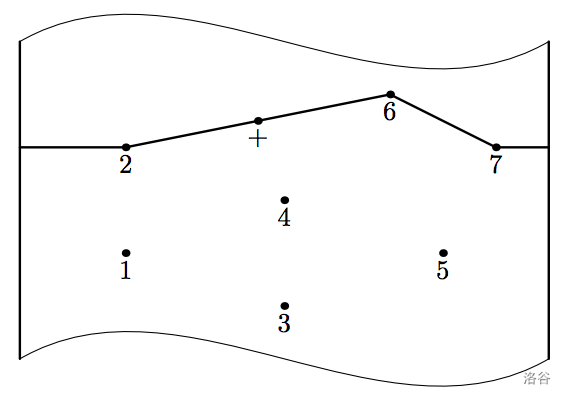
Fiona 设计了一款新的电脑游戏 **Froggy Ford**。在这个游戏中，玩家帮助一只青蛙利用河中石墩过河。青蛙从河岸跳到第一个石墩，然后跳到第二个石墩，依此类推，直到到达对岸。不幸的是，青蛙相当虚弱，其跳跃距离相当有限。因此，玩家应该选择最优路径——即最小化完成该路径所需的最大跳跃距离的路径。 :::align{center}  最优路径  添加石墩后的最优路径 ::: Fiona 认为这个游戏还不够有挑战性，因此她计划添加在河中放置一个新石墩的功能。她请你编写一个程序，确定新石墩的位置，使得完成最优路径所需的最大跳跃距离最小化。

输入文件的第一行包含两个整数 $w$ ——河的宽度，以及 $n$ ——河中石墩的数量 $(1 \le w \le 10^{9}, 0 \le n \le 1000)$。 接下来的 $n$ 行，每行包含两个整数 $x_{i}, y_{i}$ ——石墩的坐标 $(0 < x_{i} < w , −10^{9} \le y_i \le 10^{9})$。所有石墩的坐标互不相同。河岸的坐标为 $x = 0$ 和 $x = w$。

向输出文件写入两个实数 $x_{+}$ 和 $y_{+} (0 < x_{+} < w , −10^{9} \le y_{+} \le 10^{9})$ ——要添加的石墩的坐标。该石墩应能使完成最优路径所需的最大跳跃距离最小化。如果新石墩无法对最优路径提供任何改进，则可以输出满足约束的任意一对 $x_{+}$ 和 $y_{+}$，甚至可以与现有某个石墩的坐标重合。你的答案应精确到小数点后三位。

Time limit: 1 s, Memory limit: 256 MB.