P6991 [NEERC 2014] Gomoku

这是一道 IO 交互题。

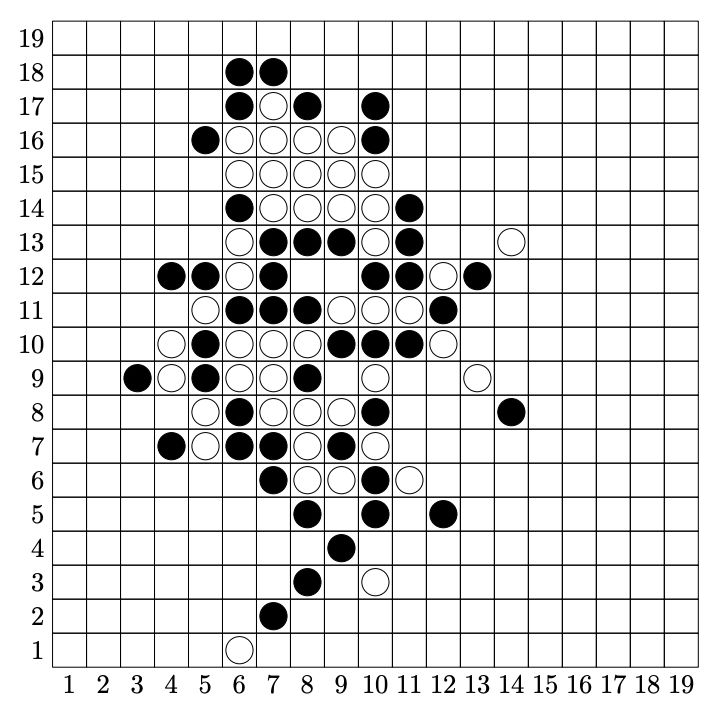
这是一个交互式问题。 五子棋是一种在二维网格上进行的双人游戏。网格的每个单元格可以是空的，包含第一位玩家的标记（黑色），或者包含第二位玩家的标记（白色），但不能同时包含两者。最初整个网格是空的。两位玩家轮流下棋，从第一位玩家开始。每次移动时，玩家可以在一个空单元格中放置她的标记。第一个在一行中有五个相邻标记的玩家获胜。获胜的行可以是垂直的、水平的或对角线的。  第二位玩家（白色标记）获胜的位置。 在这个问题中，玩家使用一个 $19 \times 19$ 的网格。如果整个网格被标记填满但没有玩家获胜，游戏被判为平局。 第一位玩家使用以下策略：作为第一次移动，她将她的标记放在网格的中心单元格。在每次其他移动中，她选择一个能最大化结果位置得分的移动。 为了找到一个位置的得分，第一位玩家考虑所有可能最终形成获胜组合的位置——换句话说，棋盘上所有水平、垂直和对角线的五个连续单元格的行（当然，它们可能相互重叠）。如果这样的行同时包含第一位玩家和第二位玩家的标记，则不予考虑。如果这样的行不包含任何标记，也不予考虑。对于每个只包含第一位玩家的标记且没有第二位玩家标记的行，添加 $50^{2k-1}$ 到位置的得分，其中 $k$ 是第一位玩家的标记数量（$1 \le k \le 5$）。对于每个只包含第二位玩家的标记且没有第一位玩家标记的行，从位置的得分中减去 $50^{2k}$。最后，随机添加一个介于 $0$ 和 $50^{2} - 1$ 之间的整数到得分中。这个随机数是均匀选择的。 在第一位玩家的几个移动得分相等的情况下（由于上述随机加法，这种平局很少见），第一位玩家选择 x 坐标最小的移动，如果 x 坐标相同，则选择 y 坐标最小的移动。 你的任务是编写一个程序，扮演第二位玩家并击败这种策略。 你的程序将与上述策略进行 100 场比赛，使用不同的随机生成器种子。你的程序必须赢得所有这些比赛。

时间限制：2 秒，内存限制：512 MB。 题面翻译由 ChatGPT-4o 提供。