P7091 数上的树

**本题自动开启 O2 优化，时间限制 2s。**

您需要构造一棵二叉树，根节点权值为 $n$，每个节点都有 $2$ 个或 $0$ 个儿子，且满足如下限制： 若该点有两个儿子，该点权值需等于两个儿子的权值之积。 若该点没有儿子，则该节点权值需为质数。 同时会给出 $m$ 条限制 $a_i$，表示树上的权值不能出现 $a_i$。 您构造的二叉树需要使：令 $k$ 为节点数， $\sum\limits_{i=1}^k\sum\limits_{j=i}^kval_{lca(i,j)}$ 最小，其中 $val_i$ 表示第 $i$ 个点的权值，$lca(i,j)$ 表示 $i,j$ 的最近公共祖先。

第一行两个正整数 $n,m$。 之后一行 $m$ 个数 $a_i$。

一行一个数，表示最小的 $\sum\limits_{i=1}^k\sum\limits_{j=i}^kval_{lca(i,j)}$。 无解输出 `-1`。

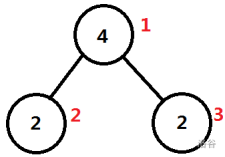
样例解释： 样例 $1$：最优方案如下：  其中，黑色数字代表权值，红色数字代表标号（您不需要对树标号，这里的标号只是为了更方便解释样例）。 $ans=val_{lca(1,1)}+val_{lca(1,2)}+val_{lca(1,3)}+val_{lca(2,2)}+val_{lca(2,3)}+val_{lca(3,3)}$ $~~~~~~~~=val_1+val_1+val_1+val_2+val_1+val_3$ $~~~~~~~~=4+4+4+2+4+2=20$ Subtask 1（5 分）： $n\leq 20$。 Subtask 2（12 分）：$n\leq 10^6$。 Subtask 3（28 分）：$n\leq 10^{12}$。 Subtask 4（20 分）：$m=0$。 Subtask 5（35 分）：$n\leq 10^{15}$。 对于所有数据 $2\leq n\leq 10^{15}$，$0\leq m\leq \min(n,10^5)$，$2\leq a_i\leq n$， 且答案不超过 $4\times 10^{18}$。