P7105 「C.E.L.U-01」门禁

abruce 有一次去机房去得**比较**早，然后……他在外面等了35分钟……于是，他想到这样一个问题： 机房的大门锁着，有 $n$ 名学生都需要进来，进来必须要门禁卡。但有些学生会一同前往。一同前往的人中只要有一个人带了门禁卡就会免于被锁在外面的窘境。现在老师终于要发门禁卡了，可是究竟要发多少张呢？

我们将题目背景中的问题简化。给出 $n$ 个点，以及任意两个点 $i,j$ 之间存在一条无向边的概率 $p_{i,j}$，求图中联通块个数的期望。

第一行一个数 $n$。 第二行到第 $n+1$ 行，每行 $n$ 个实数，代表 $p_{i,j}$。测试数据保证对任意 $1\le i \le n$，$p_{i,i}=0$，对任意 $1\le i,j \le n$，$p_{i,j}=p_{j,i}$，$0\le p_{i,j}\le1$ ，输入的实数小数点后位数不超过 $3$ 位。

仅一行一个实数，表示连通块个数的期望。当你的答案与标准答案的**绝对**误差不超过 $10^{-4}$ 时算作正确。

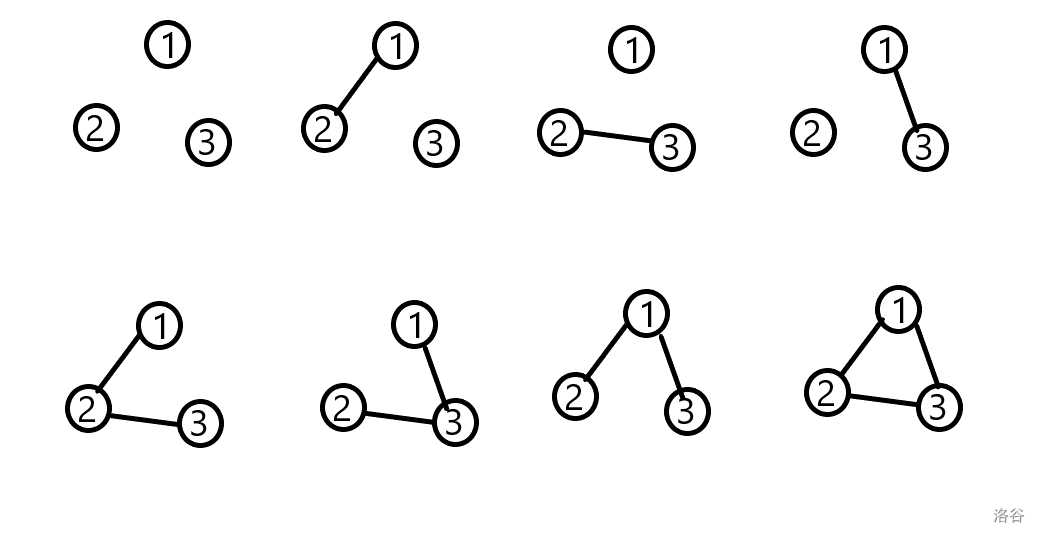
样例解释1：以下八种情况出现概率都是 $\dfrac{1}{8}$。  连通块的个数分别为 $3,2,2,2,1,1,1,1$。 所以期望是 $\dfrac{1}{8}\times3+\dfrac{3}{8}\times2+\dfrac{4}{8}\times1=\dfrac{13}{8}=1.625$ |数据编号|$n$|特殊性质| |:-:|:-:|:-:| |$1\sim3$|$\le4$|无| |$4$|$\le8$|$p_{i,j}=0$ 或 $p_{i,j}=1$| |$5\sim6$|$\le8$|$i\not=j$ 时 $p_{i,j}=0.5$| |$7\sim8$|$\le8$|无| |$9\sim10$|$\le11$|无| |$11\sim12$|$\le14$|无|