P7133 小 P 的星空
题目背景
>星依云渚溅溅,露零玉液涓涓,宝砌哀兰剪剪。碧天如练,光摇北斗阑干。
>
>—— 【元】孟昉《天净沙 · 星依云渚溅溅》
小 P 漫步于星空之下。
“摘下星星送给你,你就是我的全世界”。
“今夜,我不关心人类,我只想你”。
题目描述
将星空看作一个平面直角坐标系,小 P 所在的位置为 $(0,0)$,即坐标原点。天上共有 $n$ 颗星星,第 $i$ 颗星星的坐标为 $(x_i,y_i)$。
小 P 最初面向点 $(1,0)$,然后小 P 会进行 $m$ 次原地转动,第 $i$ 次转动后会面向点 $(u_i,v_i)$。
他可以选择逆时针转动或顺时针转动,当面向此次旋转最终将要面向的方向时,此次转动立即停止。
他相信,在转动过程中,越多的星星出现在他正前方,他【数据删除】。
小 P 想知道,每一次转动过程中他最多可以让多少星星出现在他正前方(包括转动初始方向和结束方向正前方看到的星星)。
输入格式
总共包括 $n+m+1$ 行。
第一行包含两个正整数 $n,m$,分别表示星星颗数和转动次数。
接下来的 $n$ 行,每行两个整数 $x_i,y_i$。
接下来的 $m$ 行,每行两个整数 $u_i,v_i$,意义如【题目描述】中所述。
每行的两个数字间由单个空格隔开,数据为 Linux 格式,行末保证没有多余空格。
输出格式
$m$ 行,每行一个整数。第 $i$ 行的整数表示第 $i$ 次转动的答案。
说明/提示
样例1示意图如下:
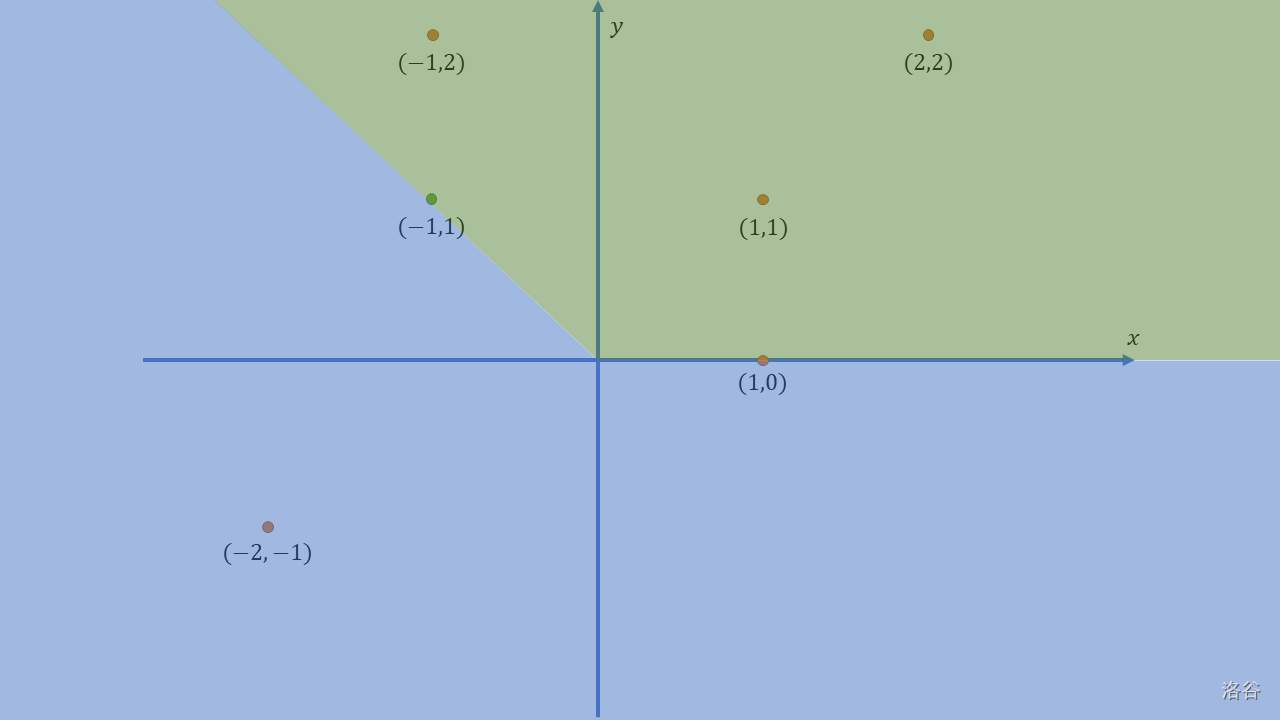
橙色点为星星,绿色点小 P 第一次的转动位置。第一次转动,从 $(1,0)$ 转到 $(-1,1)$。若顺时针转动(蓝色区域,包括边界),$(1,0)$, $(-2,-1)$,共计 $2$ 颗星星;而逆时针转动(绿色区域,包括边界),$(1,0)$, $(1,1)$,$(2,2)$,$(-1,2)$,共计 $4$ 颗星星。
第二次转动,从 $(-1,1)$ 转到 $(-1,2)$,逆时针转动,$5$ 颗星星都会在转动过程中出现在小 P 正前方。
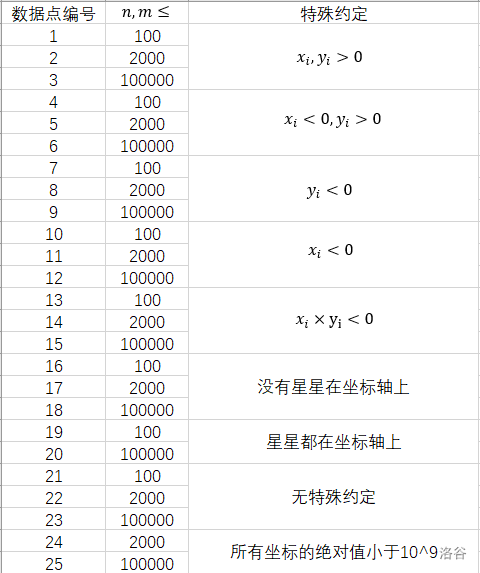
除测试点 $24$ 和 $25$ 外,其他测试点保证所有坐标的绝对值 $\le 1000$。
对于前 $12$ 个测试点,保证原点到任意星星形成的射线上没有其他星星。
除 $23,25$ 测试点外,对于所有编号为奇数的测试点,保证小 P 初始面向方向和每次转动目标方向上没有任何星星。
除 $22,24$ 测试点外,对于所有编号为偶数的测试点,保证小 P 初始面向方向和每次转动目标方向上至少有一颗星星。
对于 $100\%$ 的数据,保证星星的坐标互不相同,保证坐标不会出现 $(0,0)$,保证不会出现转动初始方向等于结束方向。
样例 $3$ 满足偶数测试点的限制。