P7177 [COCI 2014/2015 #4] MRAVI

Bobi feeds his favorite pets every morning after waking up: ants. He puts them in a glass jar with a system of pipes, which can be represented as a tree with $n$ nodes. The pipes are represented by the edges of the tree. The root of the tree is at node $1$. Inside the pipe system, due to gravity, liquid flows from a node to its children. For each pipe, we know its flow rate $x_i$: the percentage of liquid that flows from the parent node to the child node. 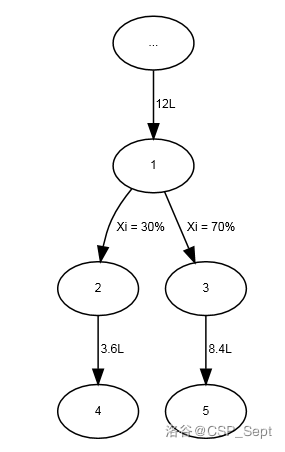Consider the following example:  In the picture, node $1$ has $12$ liters of liquid, and then there are two pipes. One has flow rate $x_i=30$, and the other has $x_i=70$. Node $2$ will receive $3.6$ liters, and node $3$ will receive $8.4$ liters. In the input, the sum of the flow rates of the pipes coming out of the same node is always equal to $100$. Some of Bobi's pipes are not normal pipes; they are a bit strange. They are super pipes, with the superpower to square the amount of liquid that flows through them. In the previous example, if the first pipe has this superpower, node $2$ receives $12.96$ liters, while node $3$ still receives only $8.4$ liters. Note that a node can have more liquid flowing out than flowing in. That is exactly why these pipes are super pipes. All super pipes can be turned on or off by Bobi. Ants live only in the leaves of the tree (nodes with no children). For each leaf, we know how much liquid is needed to feed the ants living there. Bobi wants to pour $L$ liters of liquid into the root of the tree to feed the ants. He does not have much money, so he wants to know the minimum amount of liquid he needs to buy to ensure that all ants are fed.

The first line contains an integer $n$. Each of the following $n-1$ lines contains four integers $a_i,b_i,x_i,t_i$, where $a_i$ and $b_i$ are the endpoints of the pipe (the indices of the nodes connected by the pipe), $x_i$ is the flow rate of the liquid through the pipe, and $t_i$ indicates whether the pipe has the superpower. If $t_i$ is $1$, then the pipe has the superpower; otherwise, it does not. The next line contains $n$ integers $k_i$, describing the amount of liquid required by the ants at node $i$. If node $i$ is not a leaf, then $k_i$ will be $-1$.

Output one line containing $L$. **Note: This problem uses a special judge (SPJ). Your answer is accepted if the absolute or relative error does not exceed $10^{-3}$.**

#### Explanation of Sample 1 If Bobi pours $8$ liters of liquid into the root node, node $3$ receives $4$ liters, node $4$ receives $1$ liter, and node $5$ receives $9$ liters. These nodes are leaves (where ants live), and these amounts are the minimum required by the ants. Therefore, $8$ liters is the minimum amount of liquid that satisfies the ants. #### Constraints For $100\%$ of the testdata, $1\le n\le 10^3$, $1\le a_i,b_i\le n$, $1\le x_i\le 100$, $t_i\in\{0,1\}$, and $k_i\in[1,10]$. **It is guaranteed that the value of $L$ does not exceed $2\times 10^9$.** #### Note **This problem is translated from [COCI2014-2015 CONTEST #4](https://hsin.hr/coci/archive/2014_2015/contest4_tasks.pdf) _T4 MRAVI_.** Translated by ChatGPT 5