P7181 [BalticOI 2004] Rectangles (Day2)

平面上有 $n$ 个矩形。矩形边平行于坐标轴。这些长方形可以重叠、重合或相互分离。它们的顶点坐标 $(x,y)$ 中，$x,y$ 都是非负整数，横坐标不超过 $x_{\max}$，纵坐标不超过 $y_{\max}$。 $A$ 点位于 $(0,0)$，若 $C(x_{\max},0),D(0,y_{\max}),E(x_{\max},y_{\max})$，则 $B$ 点位于线段 $CE$ 或 $DE$ 上。 线段 $AB$ 可能与矩形相交（即使只与一个矩形**顶点**相交，也视为相交）。 你需要找到一个 $B$ 点，使与线段 $AB$ 相交的矩形尽可能**多**。

第一行三个整数 $x_{\max},y_{\max},n$。 接下来 $n$ 行，每行四个整数，分别表示第 $i$ 个矩形的左下角坐标与右上角坐标。

一行三个整数，分别为： - 最多的相交矩形数； - 此时 $B$ 点坐标。 如果有多种方案，输出**任意一种**。

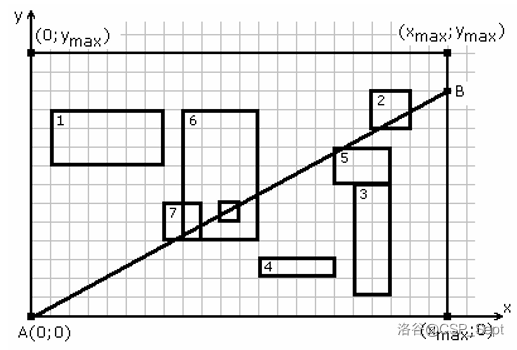
#### 样例 1 说明  输出也可以为 `5 22 11`。 #### 数据规模与约定 对于 $100\%$ 的数据，有 $1\le n\le 10^4$，$0\le x_{\max},y_{\max}\le 10^9$。 #### 说明 译自 [BalticOI 2004 Day2 B Rectangles](https://boi.cses.fi/files/boi2004_day2.pdf)。 #### 特别感谢 感谢 @[tiger2005](https://www.luogu.com.cn/user/60864) 提供的 SPJ！