P7181 [BalticOI 2004] Rectangles (Day2)

There are $n$ rectangles on a plane. Their sides are parallel to the coordinate axes. These rectangles may overlap, coincide, or be separated. For each vertex coordinate $(x,y)$, both $x$ and $y$ are non-negative integers. The $x$-coordinate does not exceed $x_{\max}$, and the $y$-coordinate does not exceed $y_{\max}$. Point $A$ is at $(0,0)$. Let $C(x_{\max},0)$, $D(0,y_{\max})$, and $E(x_{\max},y_{\max})$. Then point $B$ lies on segment $CE$ or $DE$. Segment $AB$ may intersect rectangles (even if it intersects only a rectangle **vertex**, it is still considered an intersection). You need to find a point $B$ such that the number of rectangles intersected by segment $AB$ is as **large** as possible.

The first line contains three integers $x_{\max}, y_{\max}, n$. The next $n$ lines each contain four integers, representing the lower-left corner coordinates and the upper-right corner coordinates of the $i$-th rectangle.

Output one line with three integers, in order: - the maximum number of intersected rectangles; - the coordinates of point $B$ in this case. If there are multiple solutions, output **any one** of them.

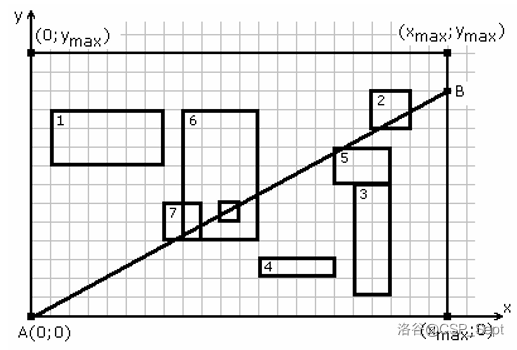
#### Sample 1 Explanation  The output can also be `5 22 11`. #### Constraints For $100\%$ of the testdata, $1 \le n \le 10^4$, $0 \le x_{\max}, y_{\max} \le 10^9$. #### Notes Translated from [BalticOI 2004 Day2 B Rectangles](https://boi.cses.fi/files/boi2004_day2.pdf). #### Special Thanks Thanks to @[tiger2005](https://www.luogu.com.cn/user/60864) for providing the SPJ! Translated by ChatGPT 5