P7220 [JOISC 2020] 掃除

JOISC2020 Day 1 T3 如果洛谷自带的下载功能无法下载错误测试点，可以在[这里](https://www.ioi-jp.org/camp/2020/2020-sp-tasks/day1/sweeping-data.zip)自行下载数据。由于测试数据过大，评测本题时，评测机可能会需要 30 秒的时间加载数据。 请注意本题不同寻常的时空限制。

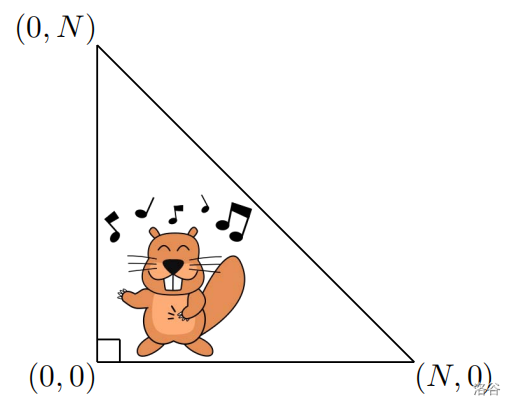
由于 Bitaro AK 了 IOI，所以 IOI 主办方送了他一套房子，为一个边长为 $N$ 的等腰直角三角形。房间内一点用坐标 $(x,y)$ 表示，其中 $0\leq x+y\leq N$。直角顶点为原点，三角形两腰分别为 $x$ 轴与 $y$ 轴。  一天，Bitaro 发现自己已经 AK 了 1919810 届 IOI 闲的没事做准备打扫房间里的灰尘。这些灰尘一开始一共有 $M$ 堆，其中第 $i$ 堆位于 $(X_i,Y_i)$。同时，可能存在多堆灰尘位于同一个位置上的情况。 现在 Bitaro 准备用扫帚打扫房间。我们认为扫帚是放置在房间里的一条线段，并且将这条线段的长度称为扫帚的宽度。由于 Bitaro 很有条理，所以他只会用以下的两种方式打扫房间： - Bitaro 将扫帚平行于 $y$ 轴放置，一端位于原点。然后他会垂直向右移动扫帚，直到不能移动为止。如果扫帚的宽度为 $l$，那么原来一堆满足 $x

第一行三个整数，分别为 $N,M,Q$。 接下来 $m$ 行，每行两个整数 $X_i,Y_i$，表示第 $i$ 堆灰尘一开始的位置。 接下来 $Q$ 行，每行两到三个整数，表示一个事件。设 $T_i$ 为第一个整数，每行含义如下： - 如果 $T_i=1$，则这行有两个整数 $T_i,P_i$，表示 Bitaro 要计算第 $P_i$ 堆灰尘的坐标； - 如果 $T_i=2$，则这行有两个整数 $T_i,L_i$，表示 Bitaro 用宽度为 $L_i$ 的扫帚进行了过程 H； - 如果 $T_i=3$，则这行有两个整数 $T_i,L_i$，表示 Bitaro 用宽度为 $L_i$ 的扫帚进行了过程 V； - 如果 $T_i=4$，则这行有三个整数 $T_i,A_i,B_i$，表示一堆新的灰尘出现在 $(A_i,B_i)$ 位置。

对于每个 $T_i=1$ 的事件，输出一行两个整数，表示事件 $i$ 发生时第 $P_i$ 堆灰尘的位置坐标。

### 样例 1 解释 一开始第一堆灰尘位于 $(1,1)$，第二堆灰尘位于 $(4,0)$。图一描述了房间现在的情况。  在第一个事件中，添加了 $(2,3)$ 位置上的第三堆灰尘。图二描述了房间现在的情况。  在第二个事件中，Bitaro 用宽度为 $3$ 的扫帚进行了过程 V。之后，第一堆灰尘移动到了 $(1,3)$，图三描述了房间现在的情况。  在第三个事件中，Bitaro 计算了第一堆灰尘的坐标 $(1,3)$。 在第四个事件中，添加 $(1,2)$ 位置上的第四堆灰尘。图四描述了房间现在的情况。  在第五个事件中，Bitaro 用宽度为 $3$ 的扫帚进行了过程 H，第一堆灰尘移到了 $(3,3)$，第三堆灰尘移到了 $(3,3)$，第四堆灰尘移到了 $(3,2)$。图五描述了房间现在的情况。  在第六个事件中，Bitaro 用宽度为 $0$ 的扫帚进行了过程 H，第二堆灰尘移到了 $(6,0)$。图六描述了房间现在的情况。  在第七个事件中，Bitaro 计算了第四堆灰尘的坐标 $(3,2)$。 在第八个事件中，Bitaro 用宽度为 $2$ 的扫帚进行了过程 V，然而什么都没有发生。图七描述了房间现在的情况。  在第九个事件中，Bitaro 计算了第三堆灰尘的坐标 $(3,3)$。 在第十个事件中，Bitaro 计算了第二堆灰尘的坐标 $(6,0)$。 这组样例满足子任务 1 和子任务 5 的限制。 #### 样例 2~5 解释 第二组样例满足子任务 1,2,4,5 的限制。 第三组样例满足子任务 1,2,5 的限制。 第四组样例满足子任务 1,3,4,5 的限制。 第五组样例满足子任务 1,5 的限制。 #### 子任务 | 子任务编号 | 特殊性质 | 分值 | | :----------: | :----------: | :----------: | | Subtask 1 | $m\leq 2\times 10^3,Q\leq 5\times 10^3$ | $1$ | | Subtask 2 | $T\in\{1,2,4\}$ | $10$ | | Subtask 3 | $T\in\{1,2,3\},X_i\leq X_{i+1},Y_i\geq Y_{i+1}(1\leq i\leq m-1)$ | $11$ | | Subtask 4 | $T\in\{1,2,3\}$ | $53$ | | Subtask 5 | 无 | $25$ | 对于 $100\%$ 的数据，$1\leq n\leq 10^9,1\leq m\leq 5\times 10^5,1\leq Q\leq 10^6$。保证： - $0\leq X_i,Y_i\leq N,X_i+Y_i\leq N(1\leq i\leq m)$； - $1\leq P_i\leq M^\prime(1\leq i\leq Q)$，其中 $M^\prime$ 表示事件 $i$ 发生时灰尘的堆数； - $0\leq L_i\leq n-1(1\leq i\leq Q)$； - $0\leq A_i,B_i\leq n,A_i+B_i\leq n(1\leq i\leq Q)$； - 至少存在一个 $T_i=1$ 的事件。