P7238 迷失森林

首先给出一棵以 $1$ 为根，$n$ 个结点的树，定义为「单位树」。 现有 $n$ 个结构与「单位树」完全相同的树，要将 $n$ 个树再用 $n-1$ 条边连接起来。 为方便叙述，用符号 $(a,b)$ 表示结点 $a$ 所代表树中，编号为 $b$ 的结点。 连接方式如下： 1. 将 $n$ 棵树按照「单位树」的结构摆放好。 2. 对于每个 $i(1

第一行输入一个正整数 $n$，表示「单位树」的结点数。 接下来输入 $n-1$ 行，每行两个正整数 $u,v$，表示「单位树」中的一条边。

输出一行一个正整数，表示树上两点简单路径所包含的 **结点** 个数的最大值。

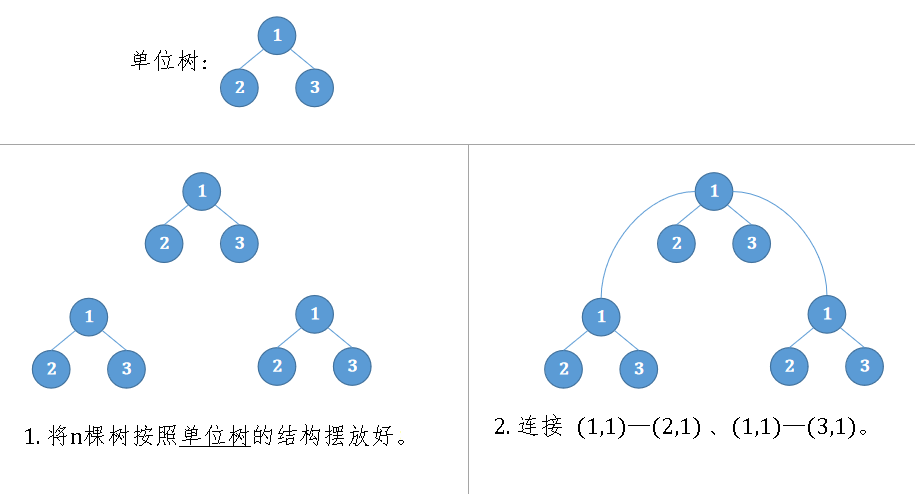
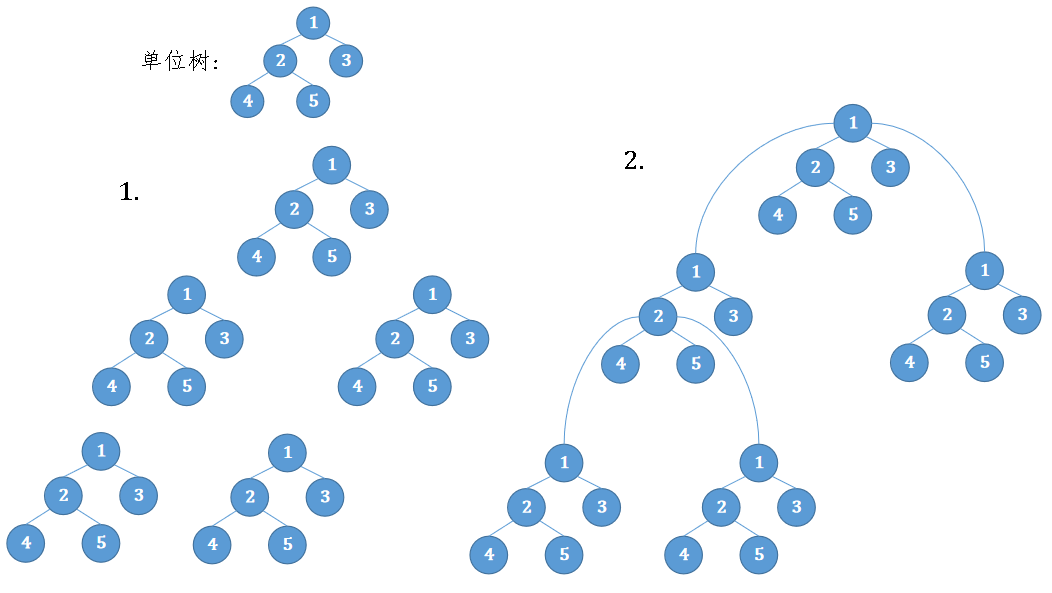
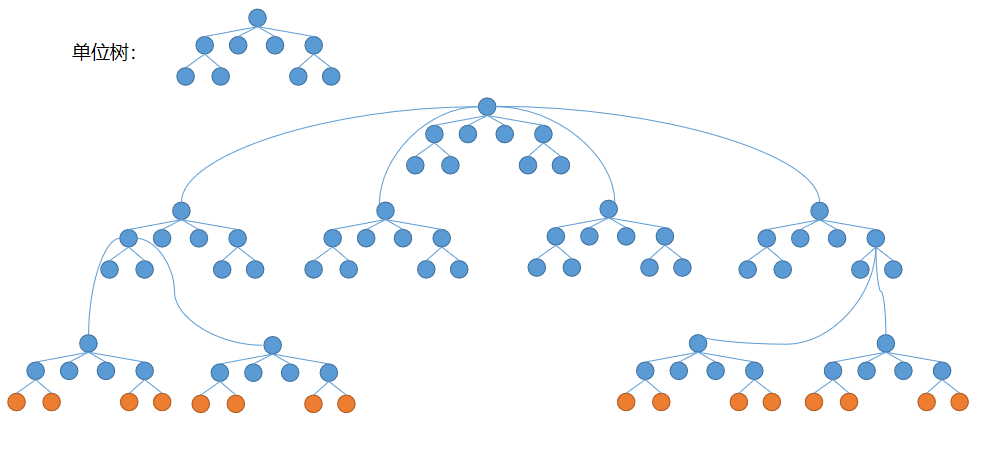
#### 样例说明 样例 #1  样例 #2 如下图，以 $(3,4)$ 和 $(4,4)$ 为两端的路径包含 $9$ 个结点，长度为 $9$。  样例 #3 如下图，取 $(6,6)$ 和 $(9,9)$，包含 $11$ 个结点。  事实上，任取两个最近公共祖先为 $1$ 的橙色结点，答案均为 $11$。 #### 数据范围 **本题采取捆绑测试。** | 子任务编号 | 分值 | $n\le$ | 特殊性质 | | :----------: | :----------: | :----------: | :----------: | | $1$ | $10$ | $10$ | $\times$ | | $2$ | $12$ | $10^6$ | $v=u+1$ | | $3$ | $6$ | $10^6$ | $u=1$ | | $4$ | $18$ | $=2^k(k\in\mathbf{Z})$ | $u=\left\lfloor\dfrac{v}{2}\right\rfloor$ | | $5$ | $27$ | $10^3$ | 树的形态随机 | | $6$ | $27$ | $10^6$ | $\times$ | 对于 $100\%$ 的数据：$1\leq n\leq10^6$，结点编号介于 $1\sim n$ 之间。 **本题可能略微卡常。** 时限缩短为 1s，原因如下： - 讨论区认为本题撞原，为防止所谓「加强版」的 $O(n\log n)$ 做法直接冲过本题，时限缩短。 - 最优解能跑进 200ms 以内。 - 由于出题人懒惰，懒得 $n\le10^6\rightarrow n\le10^7$ 只能通过缩短时限来卡掉所谓原题做法（实际上是错解）。