P7250 [BalticOI 2012] 山峰 (Day1)

有一个 $N \times M$ 大小的岛屿，每个点有不同的海拔。定义相邻为两个点横纵坐标差均不超过 $1$。定义路径为任意两个连续点都相邻的序列。定义平坦的区域是一组联通的海拔相同的点的极大集合，山峰是一个不与任何海拔更高的点相邻的平坦区域。 给出这个岛屿上每个点的海拔，你需要求出岛屿上所有的山峰与前往比其高度更高的山峰所需经过的最低点的海拔的最大值。

第一行两个整数 $N,M$，代表地图的长和宽。 接下来 $N$ 行，每行 $M$ 个整数 $E_{i,j}$ ，描述了 $(i,j)$ 的海拔。

第一行一个整数 $P$，代表岛上的山峰数。 接下来 $P$ 行，每行两个整数 $h_0,h_1$，代表某座山峰的海拔，以及从该山峰出发到达更高的山峰所需经过的最低点的海拔的最大值。 输出应以 $h_0$ 为第一关键字，$h_1$ 为第二关键字降序排列，特别的，对于最高峰，$h_1=0$

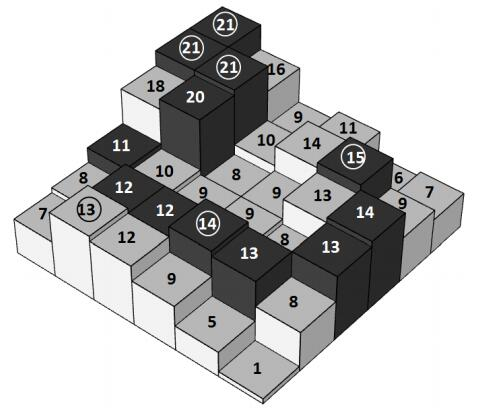
**【样例解释】**  如上图所示，其中圆圈圈出的为山峰，从海拔为15的山峰前往其他山峰的一条路径用深色标出。 **【数据范围】** - 对于 15% 的数据，满足 $\min (N,M)\leq 2$ - 对于 50% 的数据，满足 $P \leq 500$ - 对于 80% 的数据，满足 $P \leq 5000$ - 对于 100% 的数据，满足 $1 \leq N,M \leq 2000$，$N \times M \leq 10^5$，$1 \leq E_{i,j} \leq 10^6$ **【说明】** 译自 [BalticOI 2012 Day1 T3. Peaks](http://www.boi2012.lv/data/day1/eng/peaks.pdf)